DERIVADAS
Para calcular la derivada de una función debemos tener en cuenta las fórmulas que podemos encontrar en cualquier libro de 1º Bachillerato / 3º BUP. Estas son:

Ahora si queremos calcular la derivada de una función tenemos que saber que fórmula es la que debemos aplicar.
Ej.:
1.-
|
|
En este caso tenemos una multiplicación de funciones, por lo tanto debemos aplicar la fórmula del producto. |
|
|
La primera derivada que tenemos que calcular corresponde a una función potencial, y la segunda a una función logaritmo neperiano, así aplicamos la fórmulas correspondientes. |
|
|
|
2.-
|
|
De nuevo tenemos un producto de funciones, en este caso la función identidad y la función seno. |
|
|
|
3.-
|
|
Ahora tenemos una función exponencial de base el número e. |
|
|
Nos queda a resolver la derivada del producto de una constate por una función. |
|
|
|
4.-
|
|
La función a derivar es una función de tipo seno. Posteriormente debemos derivar una suma, y por último el producto de una constante por una función. |
|
|
|
5.-
|
|
Esta función es del estilo a la anterior. |
|
|
|

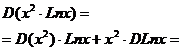
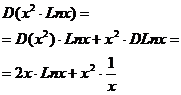
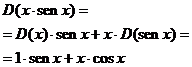

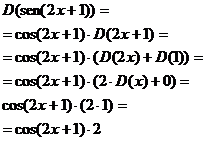
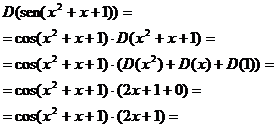
yo queria derivadas trigonometricas las ya mencionadas estan super faciles
no sirvio de nada su respuesta pendejos
es muy util
como hallar:f (x)=1-cos x