Visite nuestra página integrales.es
INICIACION A LA DERIVACIÓN
DERIVADAS UNA VARIABLE
2ª PARTE FÓRMULAS COMPUESTAS
Versión 27-2-2014
| TIPOS DE FORMULAS BÁSICAS DE DERIVACIÓN | ||
| FORMAS SIMPLES |
Nº |
FORMAS COMPUESTAS |
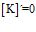 |
1 |
|
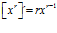 |
2 |
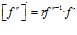 |
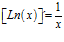 |
3 |
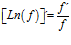 |
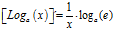 |
4 |
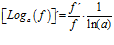 |
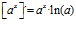 |
5 |
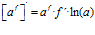 |
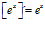 |
6 |
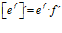 |
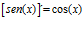 |
7 |
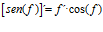 |
 |
8 |
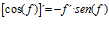 |
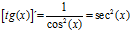 |
9 |
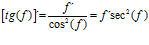 |
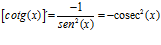 |
10 |
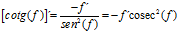 |
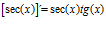 |
11 |
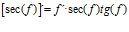 |
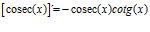 |
12 |
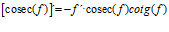 |
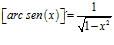 |
13 |
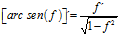 |
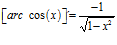 |
14 |
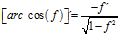 |
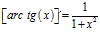 |
15 |
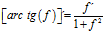 |
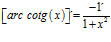 |
16 |
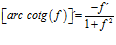 |
 |
17 |
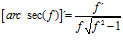 |
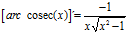 |
18 |
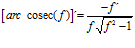 |
|
REGLAS BÁSICAS DE DERIVACIÓN |
1ª) LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función: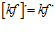 |
2ªa) LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones: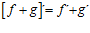 |
2ªb) LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones: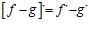 |
3ª) LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función: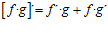 |
4ª) LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado: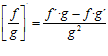 |
5ª) LA DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA es igual a la derivada de la expresión como exponencial más la derivada de la expresión como potencial: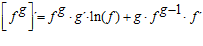 |
DERIVADA DE UNA FUNCIÓN POTENCIAL
|
FÓRMULA 2 compuesta
LA DERIVADA DE UNA FUNCIÓN POTENCIAL DE x es igual al exponente por la función de x elevada a una unidad menos por la derivada de la función |
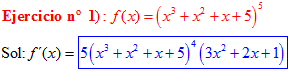
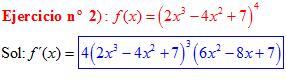
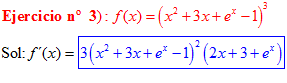
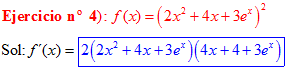
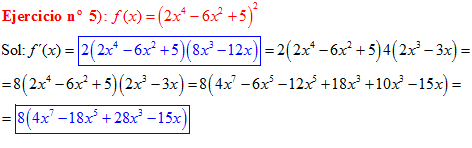
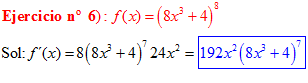
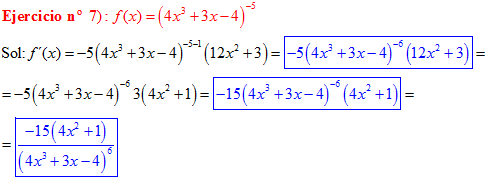
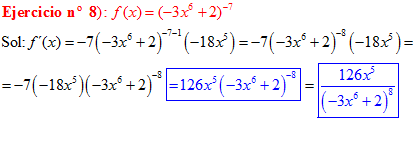
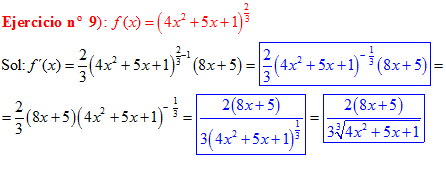
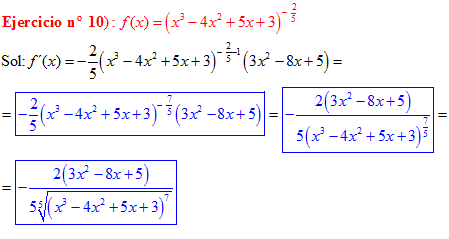

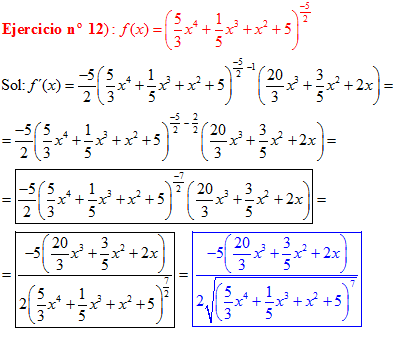

|
Recuerda siempre que:
LA DERIVADA DE LA RAIZ CUADRADA DE UNA FUNCIÓN DE x es igual a la derivada de la función de x dividida entre dos veces la raíz cuadrada de dicha función de x |
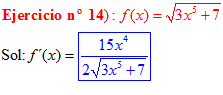
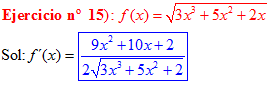

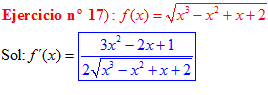
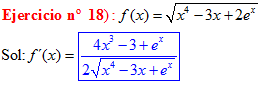
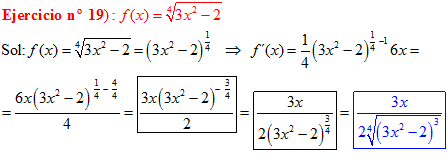
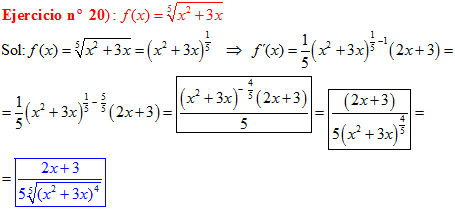

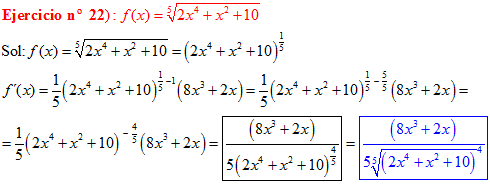
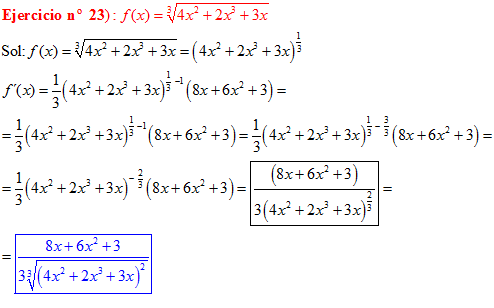
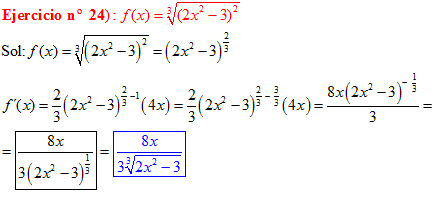
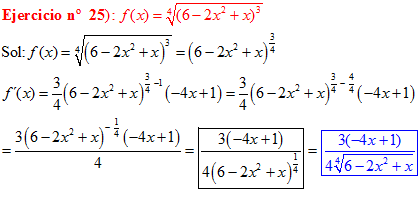
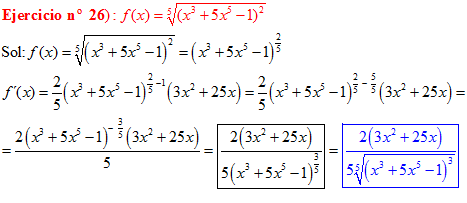
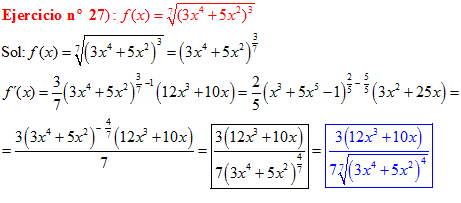
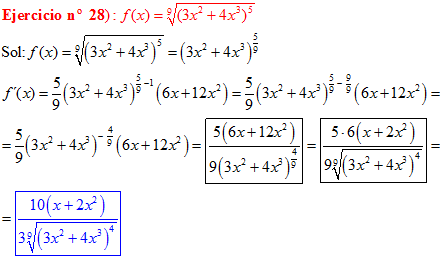
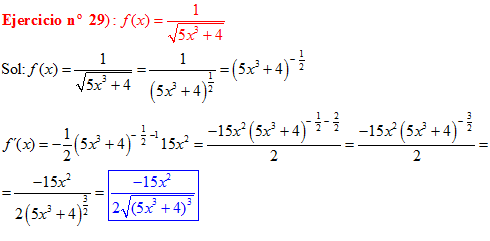
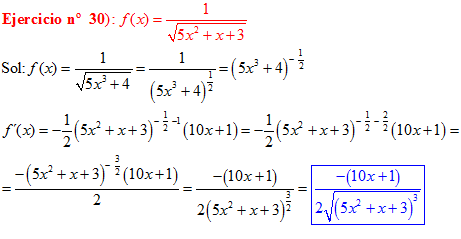
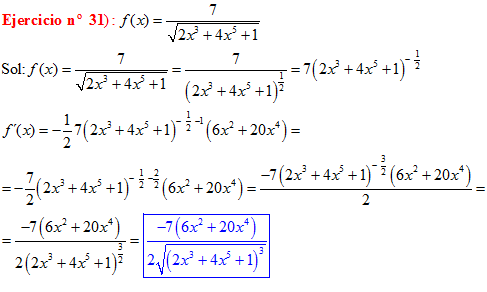

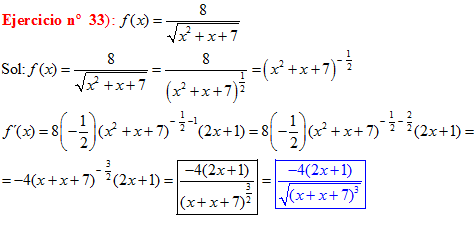
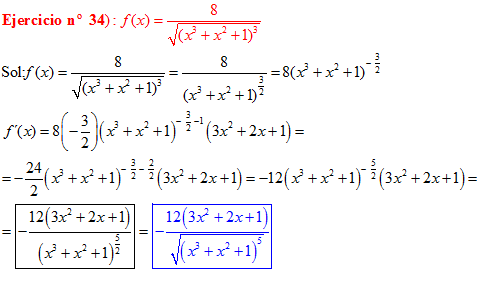
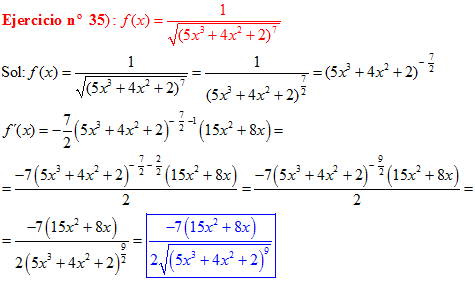
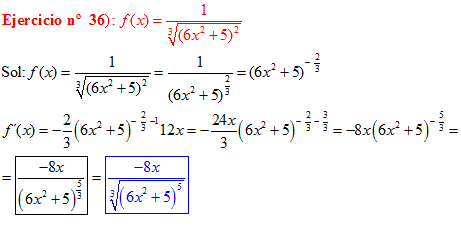
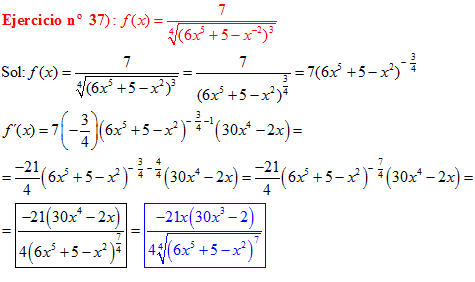
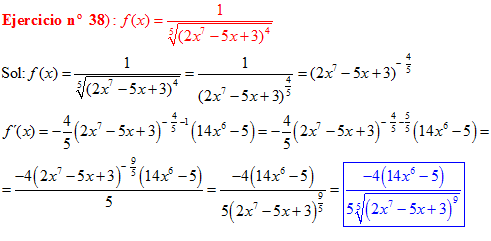
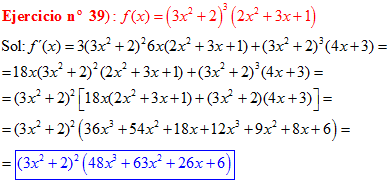
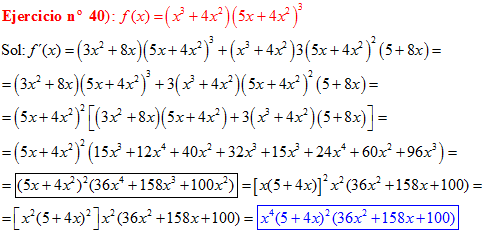
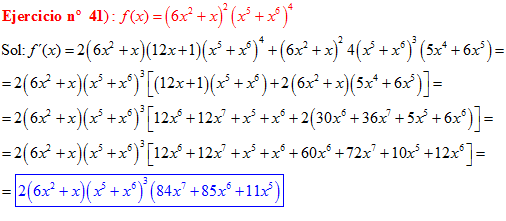
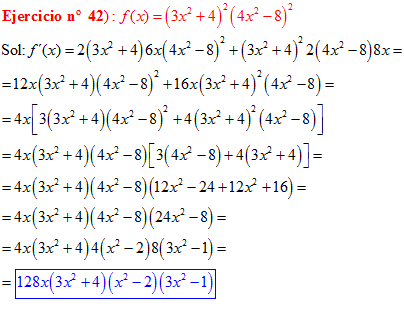
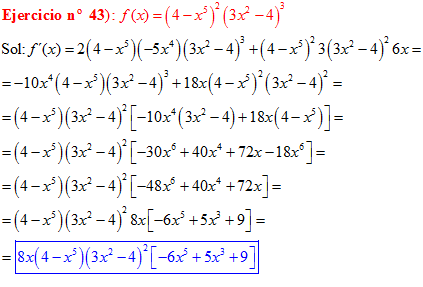



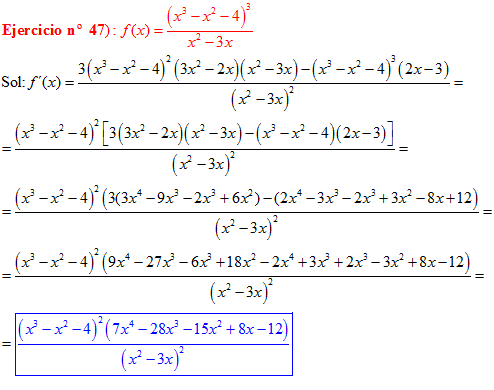
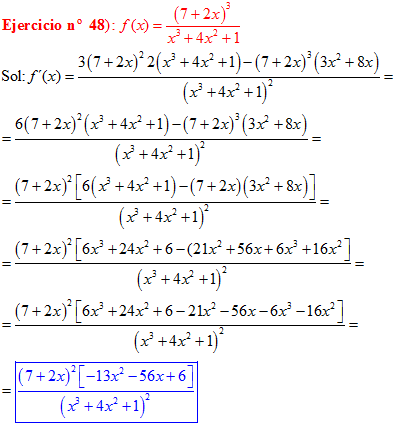
❊❊❊❊❊ FIN FÓRMULA 2 ❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN LOGARÍTMICA
|
FÓRMULA 3 compuesta
LA DERIVADA DEL LOGARITMO NEPERIANO DE UNA FUNCIÓN DE x es igual a la derivada de la función de x dividida entre dicha función |
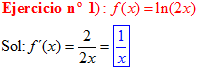
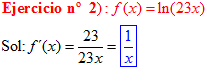
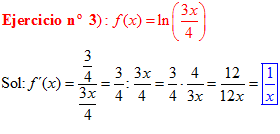
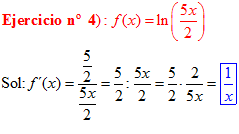
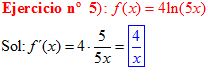
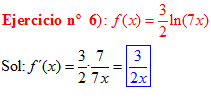
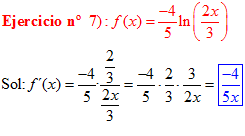
|
LOGARITMOS Recuerda de la ESO:
El LOGARITMO DE «a» ELEVADO A «b» es igual al exponente b multiplicado por el logaritmo de a |
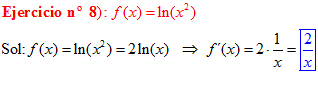
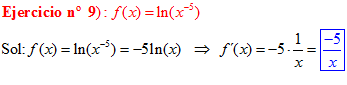
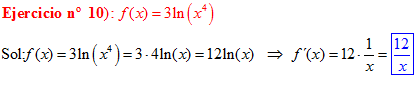
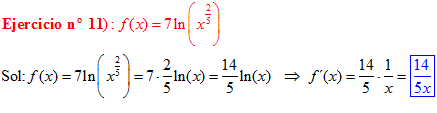
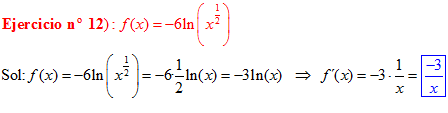
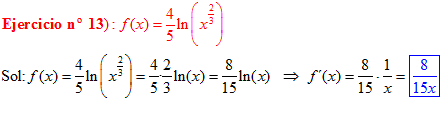
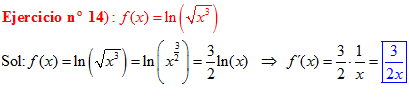
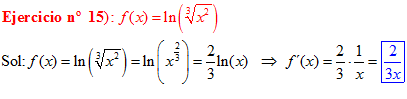
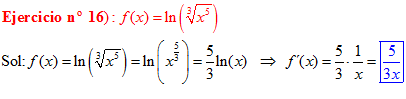
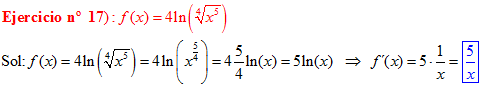
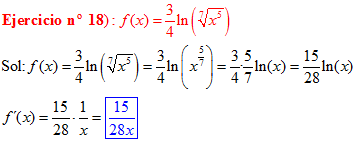
|
LOGARITMOS Recuerda de la ESO:
EL LOGARITMO NEPERIANO DE UN PRODUCTO ES: igual a la suma de los logaritmos de los factores |
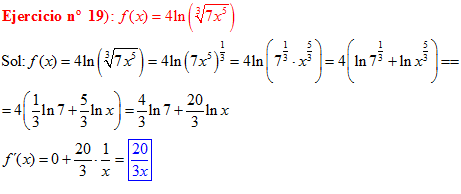
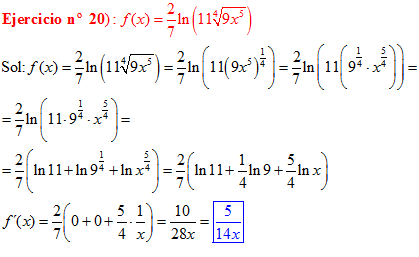
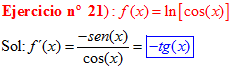
|
TRIGONOMETRÍA Recuerda de la ESO:
LA COTANGENTE DE UN ÁNGULO es igual al coseno de dicho ángulo dividido entre el seno del mismo |
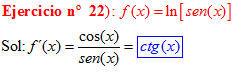
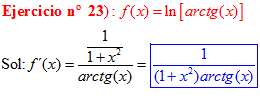
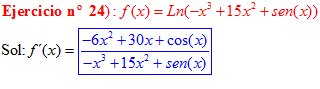
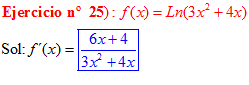
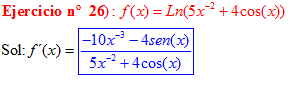
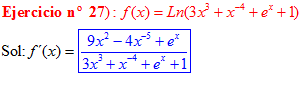
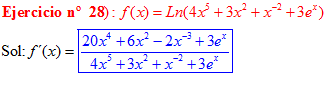
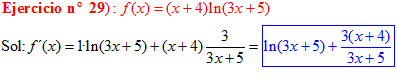
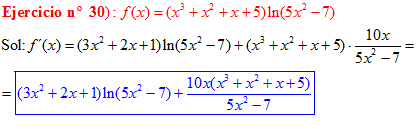
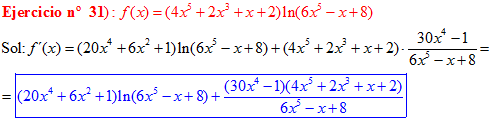
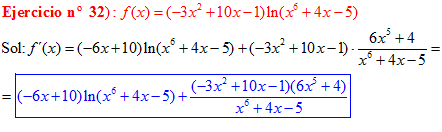
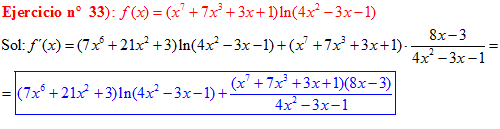
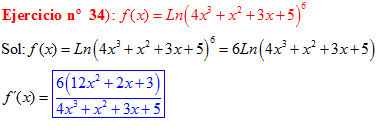
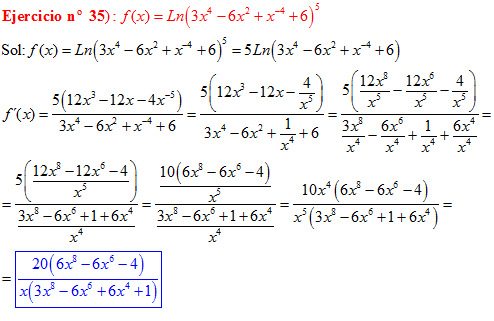
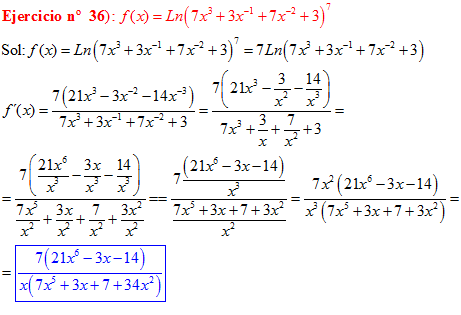
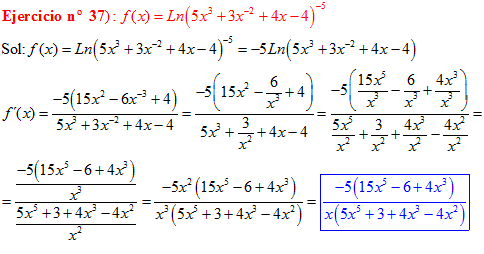
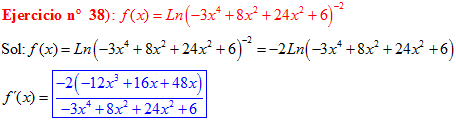
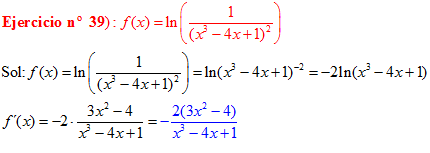
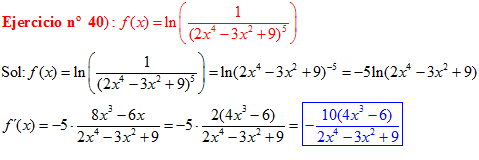
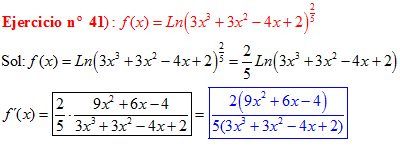
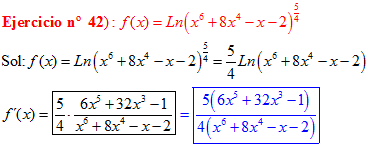
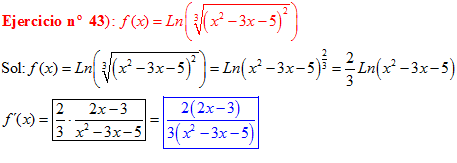
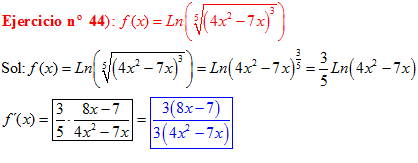
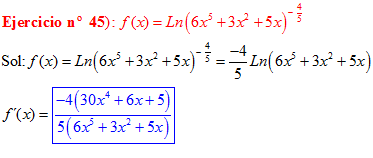
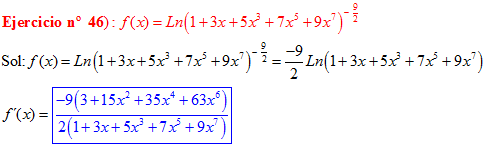
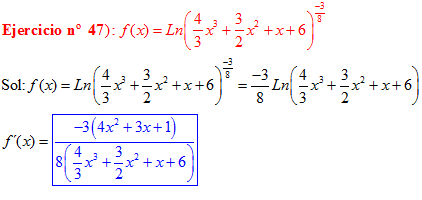
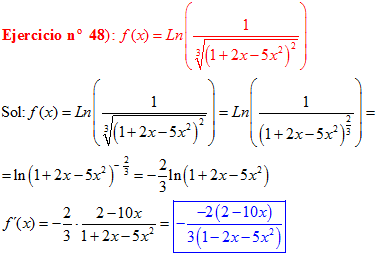
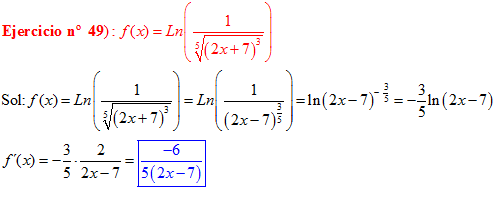
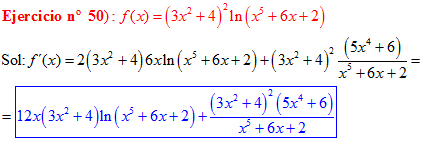
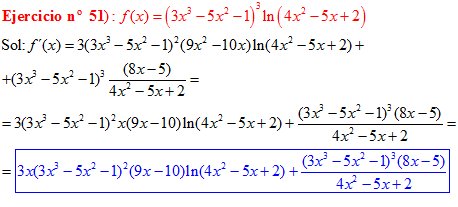
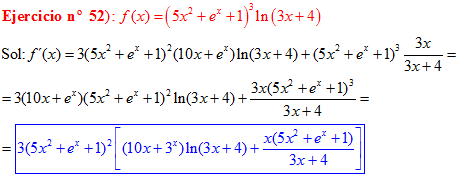
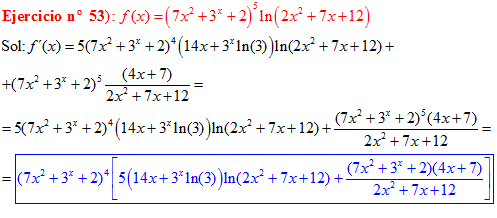
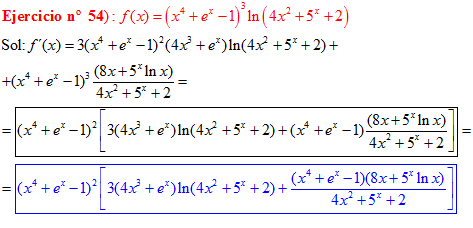


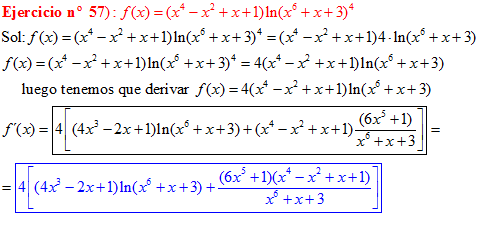

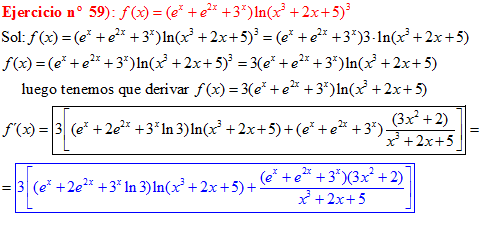

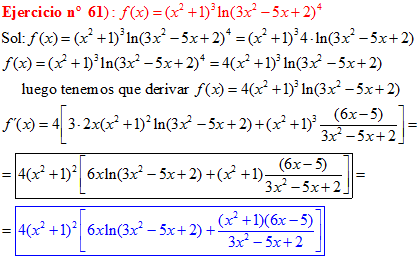



❊❊❊❊❊ FIN FÓRMULA 3 ❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN LOGARÍTMICA CON BASE DISTINTA DEL NÚMERO e
|
FÓRMULA 4 compuesta
LA DERIVADA DEL LOGARITMO EN BASE a DE UNA FUNCIÓN DE x es igual a la derivada de la función de x dividida entre dicha función por la unidad dividida por el logaritmo neperiano de a |
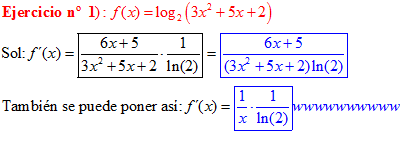
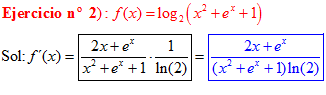
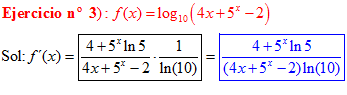
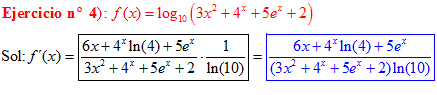
❊❊❊❊❊ FIN FÓRMULA 4 ❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN EXPONENCIAL CON BASE DISTINTA DEL NÚMERO e
|
FÓRMULA 5 compuesta
LA DERIVADA DE UN NÚMERO «a» DISTINTO DE «e» ELEVADO A UNA FUNCIÓN DE x es igual a ese número elevado a la función de x multiplicado por la derivada de dicha función y por el logaritmo neperiano del numero «a» |
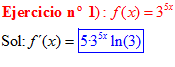
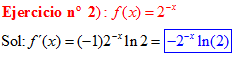
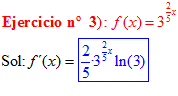
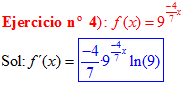
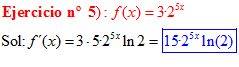
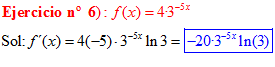
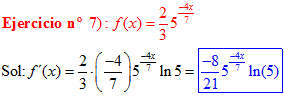
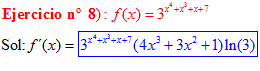
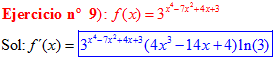
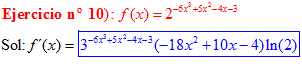
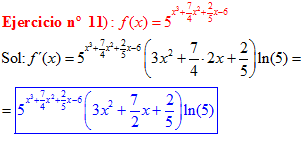
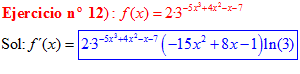
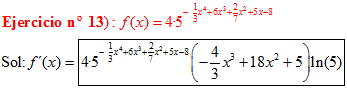
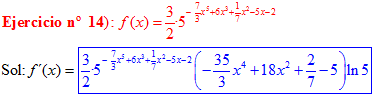
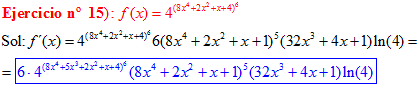

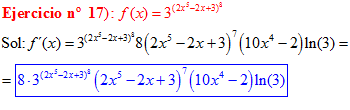
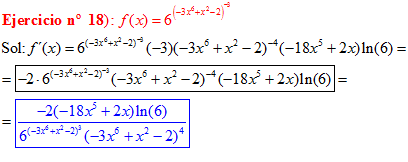
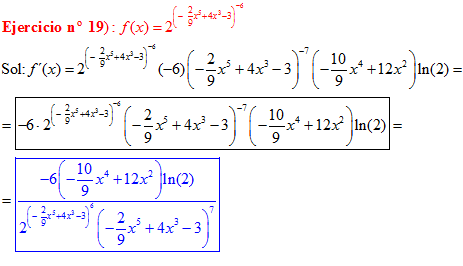
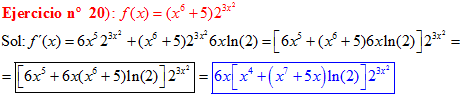
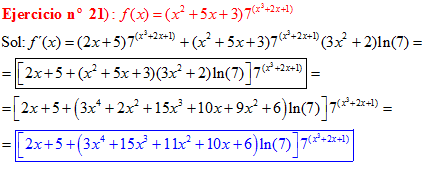
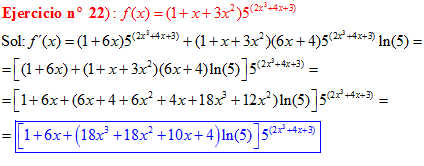
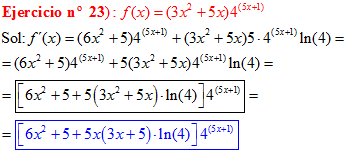
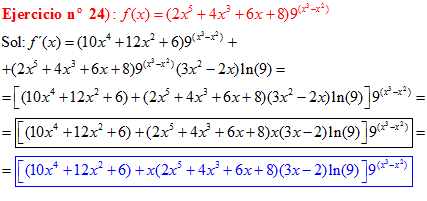
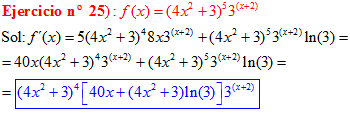
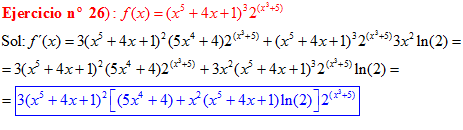
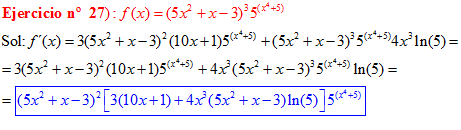
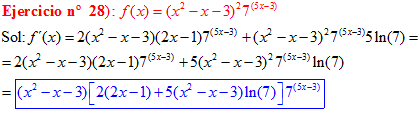
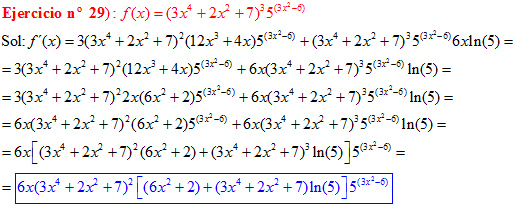
❊❊❊❊❊ FIN FÓRMULA 5 ❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN EXPONENCIAL CON BASE EL NÚMERO e
|
FÓRMULA 6 compuesta
LA DERIVADA DEL NÚMERO «e» ELEVADO A UNA FUNCIÓN DE x es igual al número «e» elevado a dicha función de x multiplicado por la derivada de dicha función |
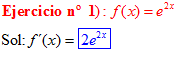
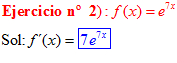
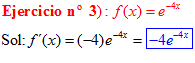
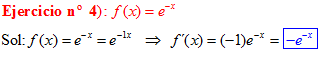
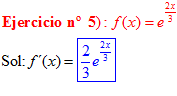
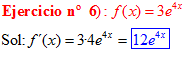
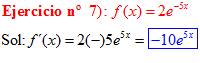
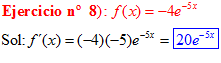
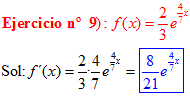
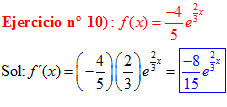
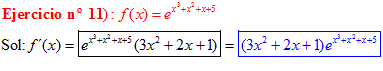
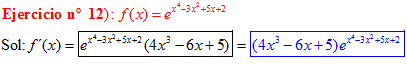
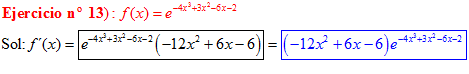
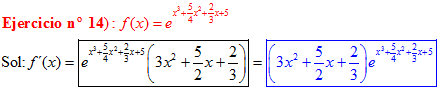
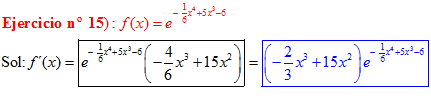
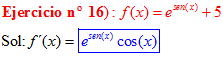
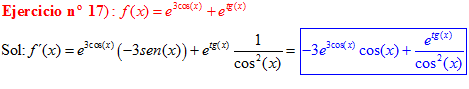
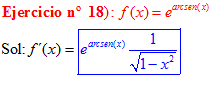
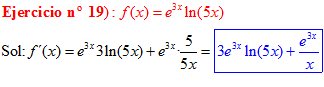
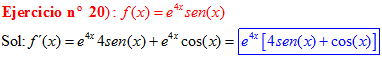
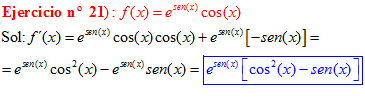
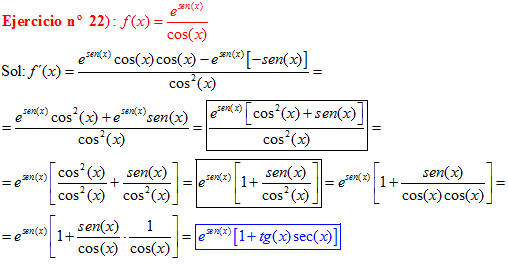
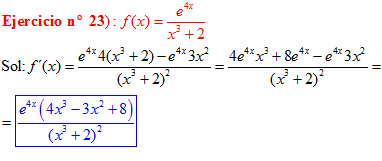
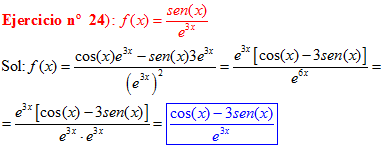

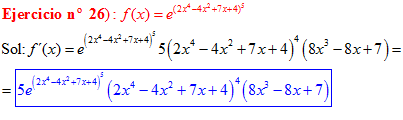
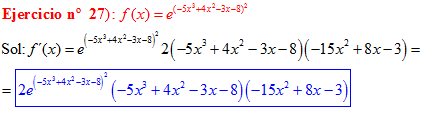
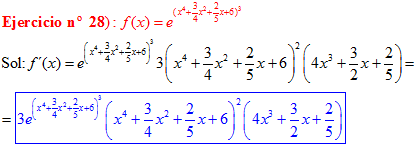
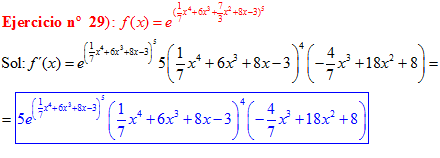
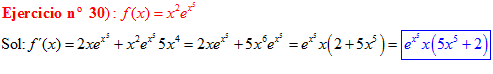
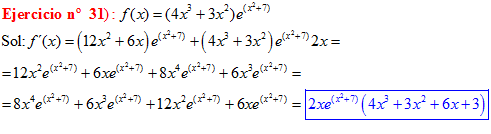
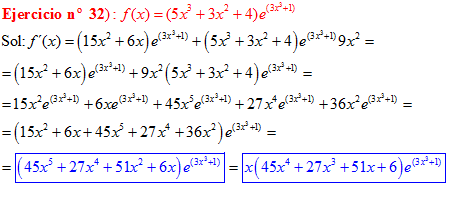
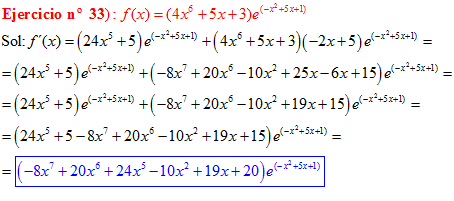

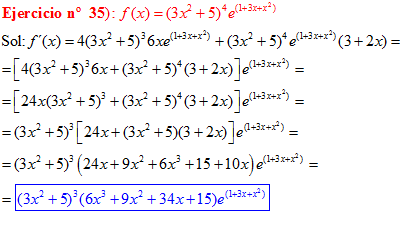
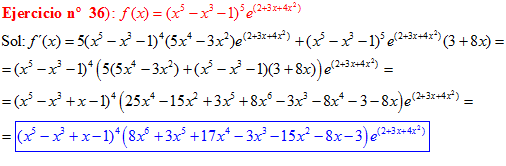
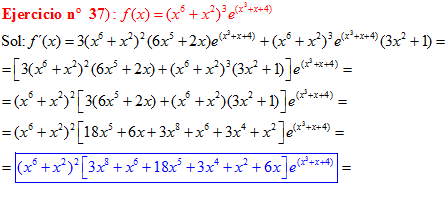
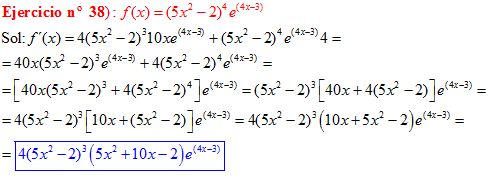
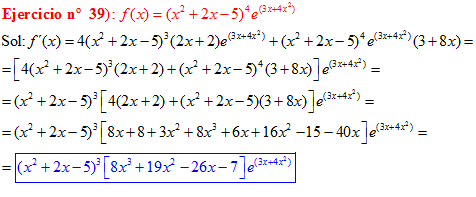
❊❊❊❊❊ FIN FÓRMULA 6 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA SENO
|
FÓRMULA 7 compuesta
LA DERIVADA DEL SENO DE UNA FUNCIÓN DE x es igual al coseno de la función de x multiplicado por la derivada de dicha función |
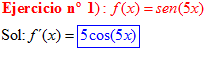

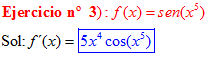
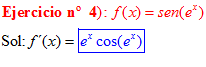
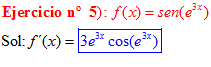
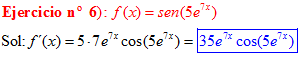
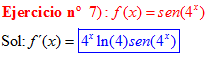
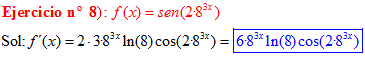
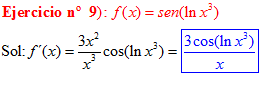
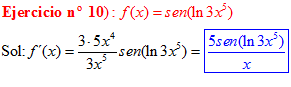
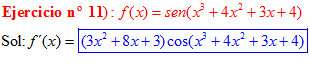

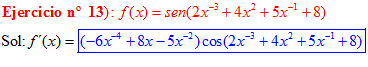
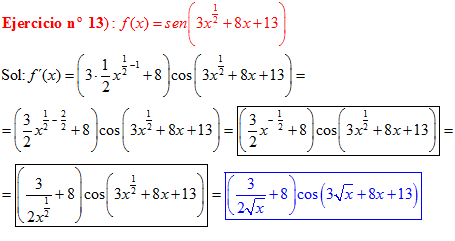
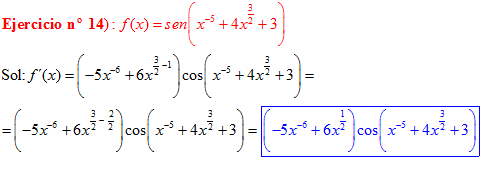
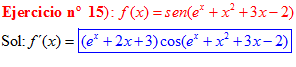
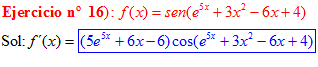
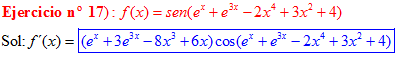
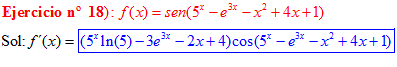
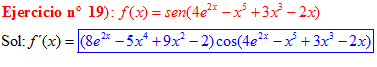
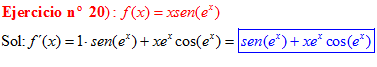
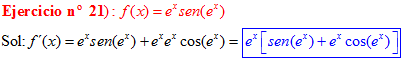
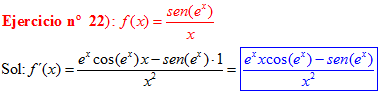
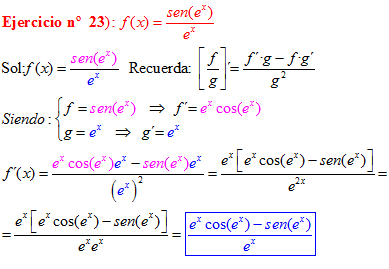
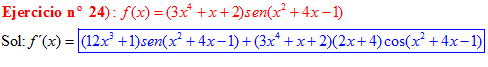
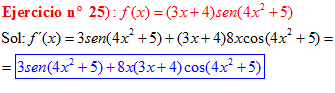
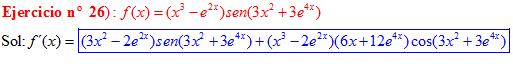
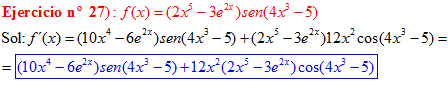
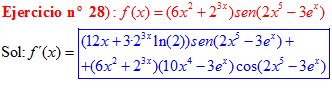
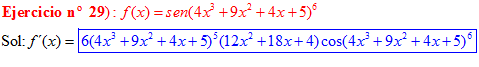
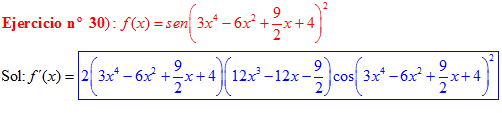
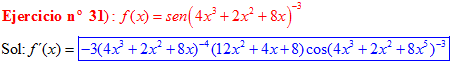
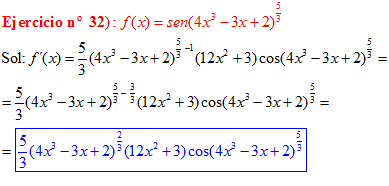
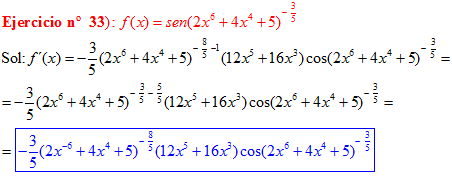
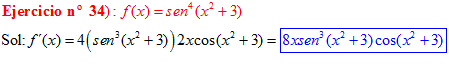
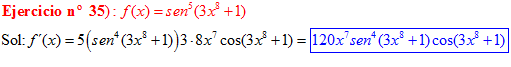
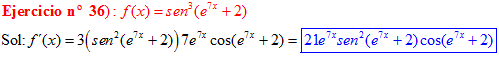
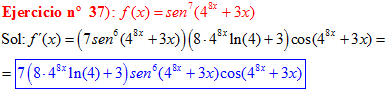

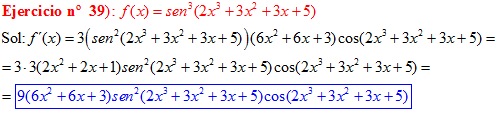
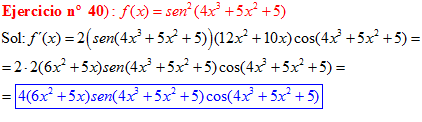
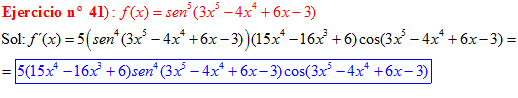
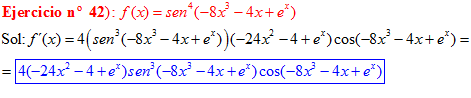
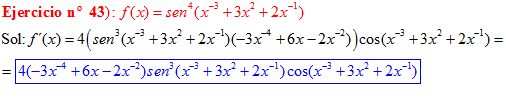
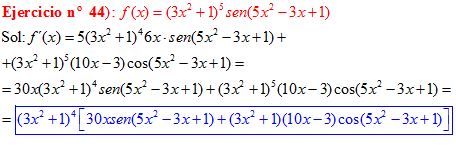
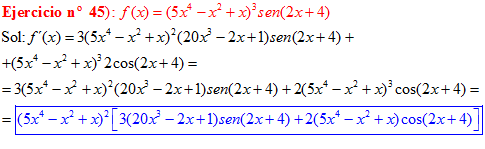
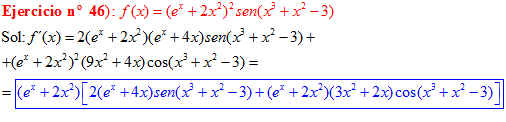
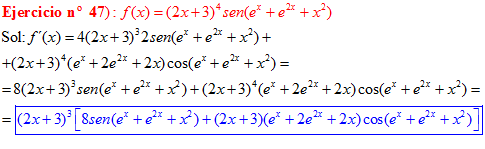
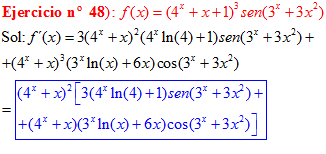
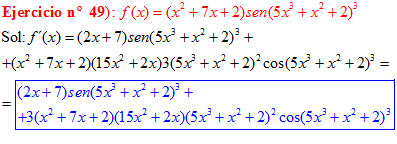
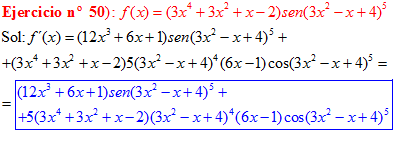
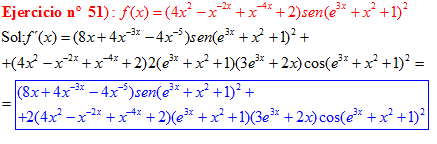
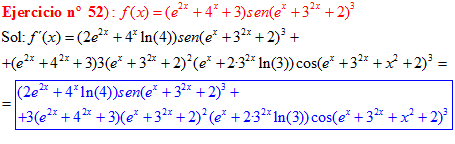
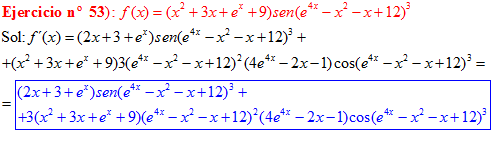
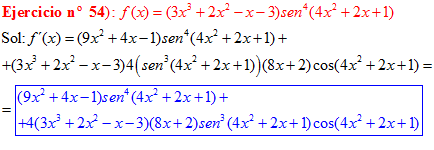
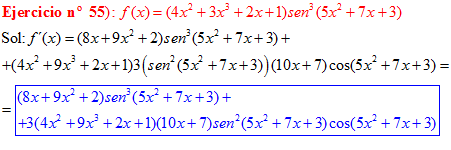
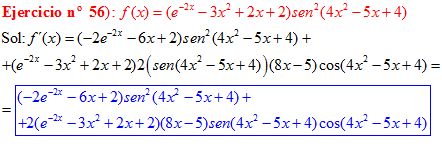
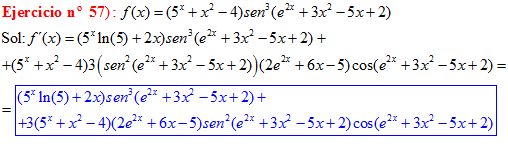
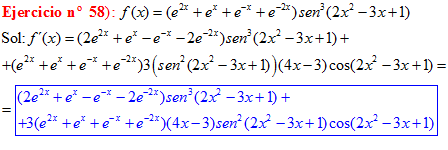
❊❊❊❊❊ FIN FÓRMULA 7 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COSENO
|
FÓRMULA 8 compuesta
LA DERIVADA DEL COSENO DE UNA FUNCIÓN DE x es igual a menos seno de la función de x multiplicado por la derivada de dicha función |
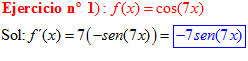
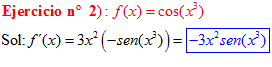
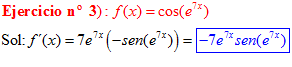
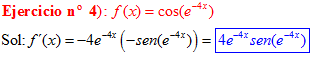
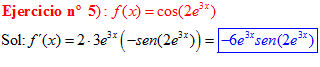
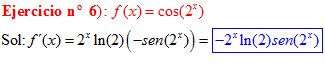
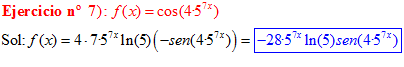
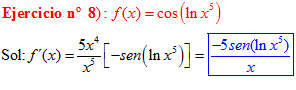
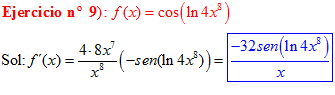
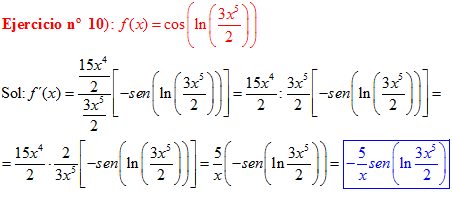
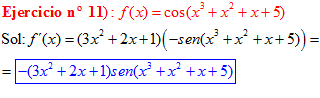
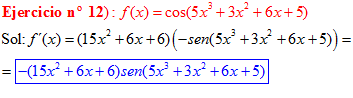
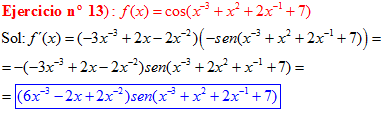

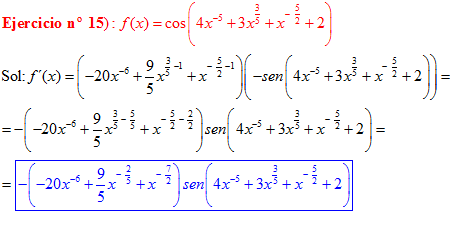
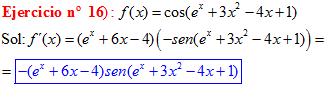
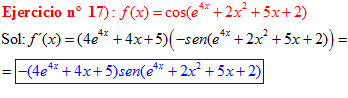
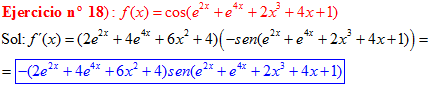

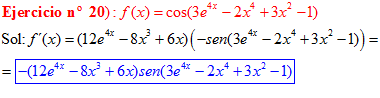
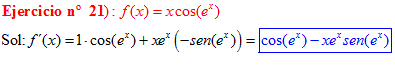
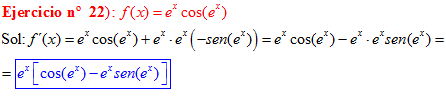


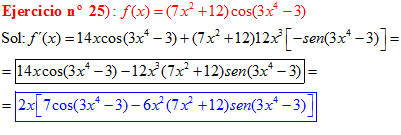
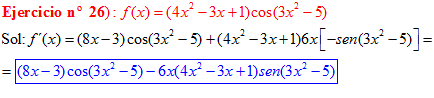
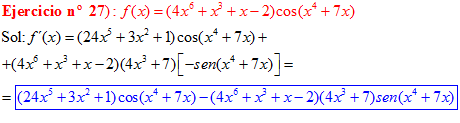
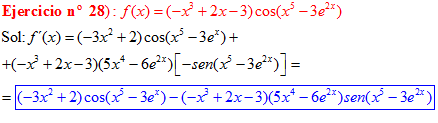
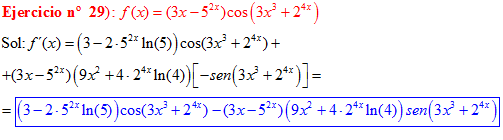
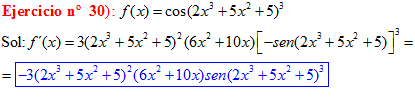
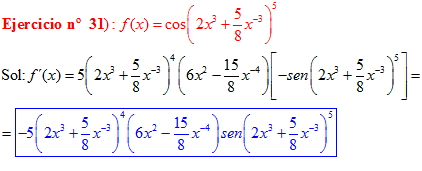
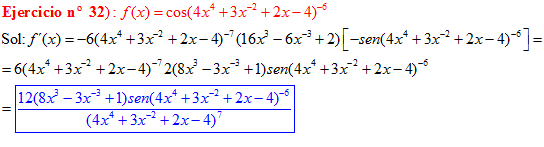

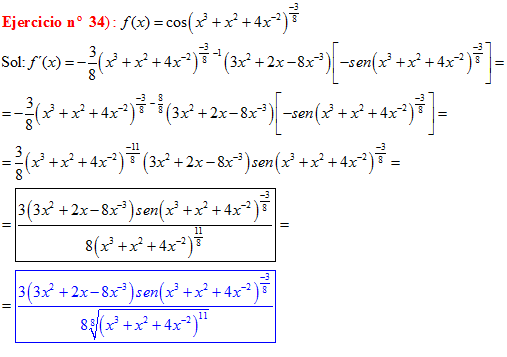
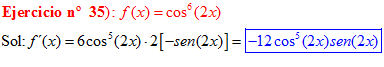
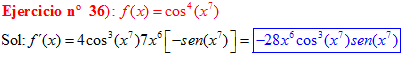
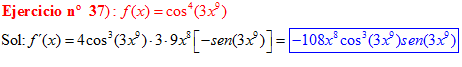
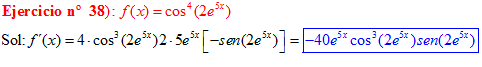
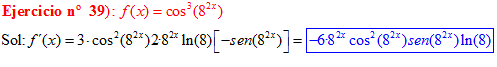
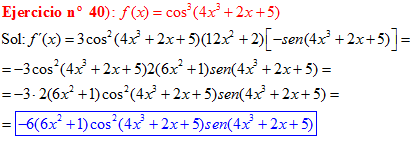
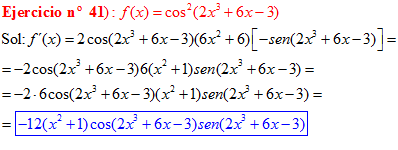
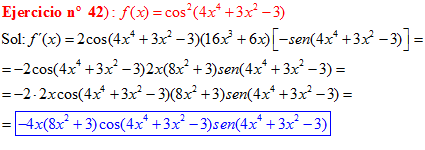
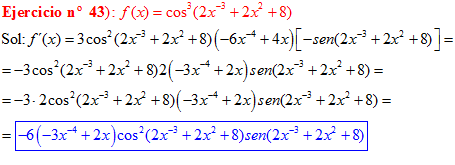
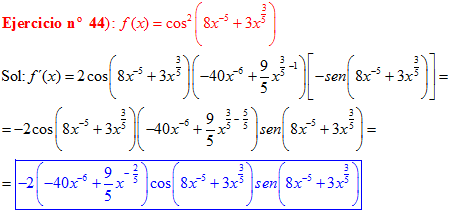
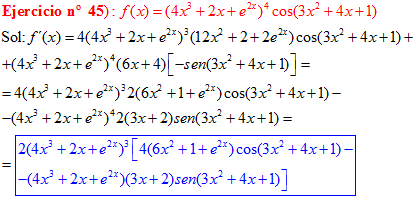
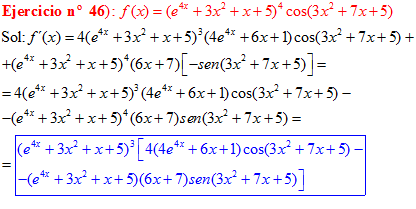
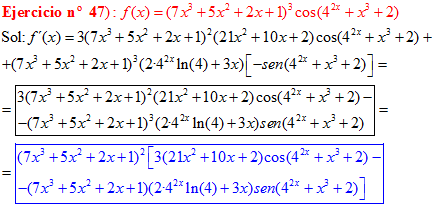
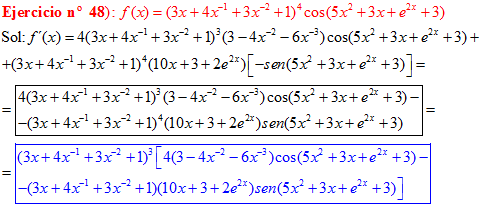
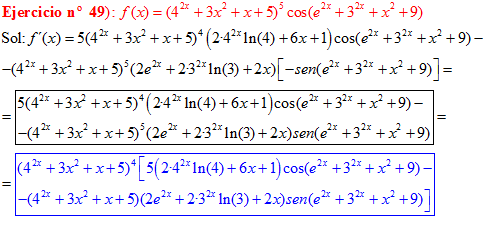
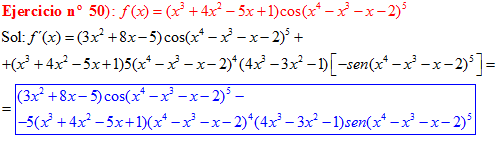
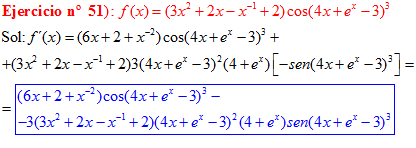
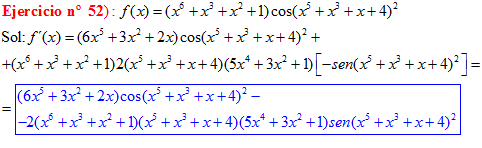
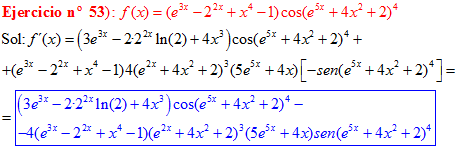
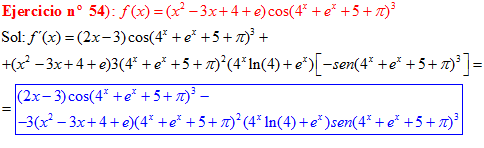
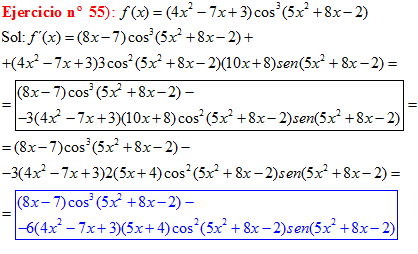
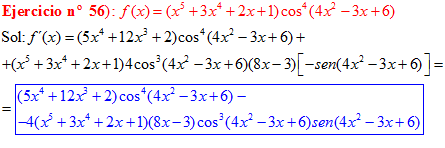
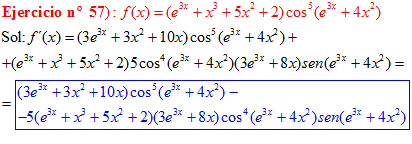
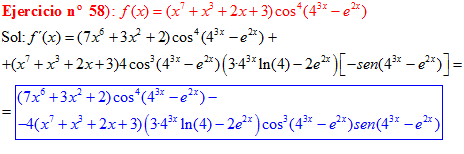
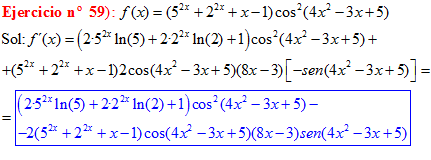
❊❊❊❊❊ FIN FÓRMULA 8 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA TANGENTE
|
FÓRMULA 9 compuesta
LA DERIVADA DE LA TANGENTE DE x es igual a la unidad dividida por el coseno cuadrado de x |
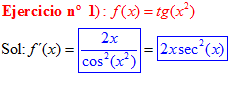
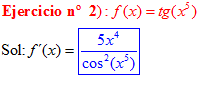
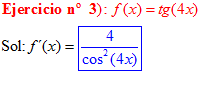
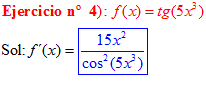
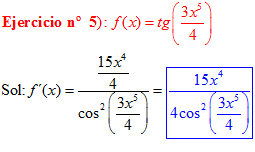
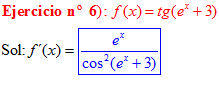

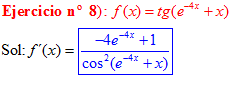
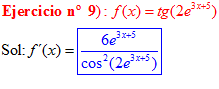
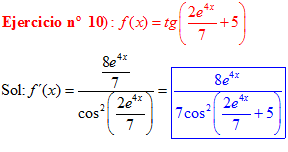
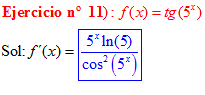
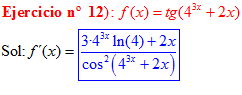
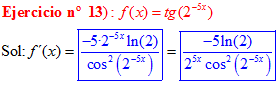
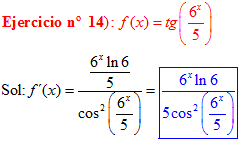
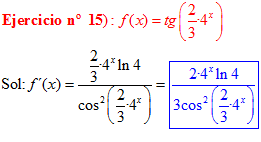
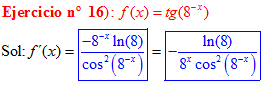
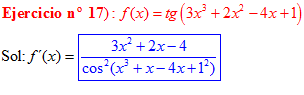
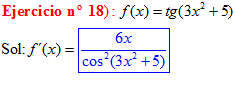
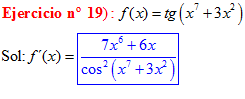

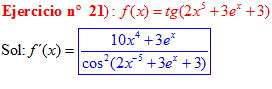
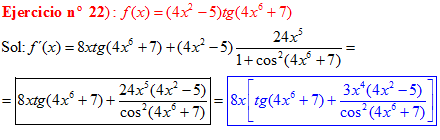
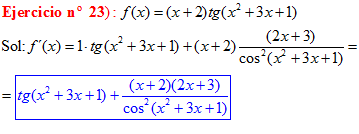
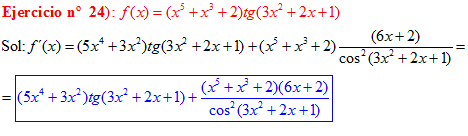
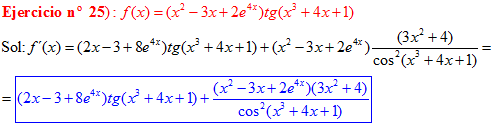
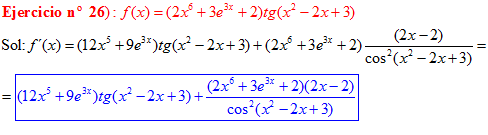
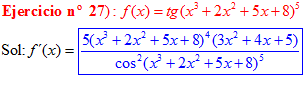
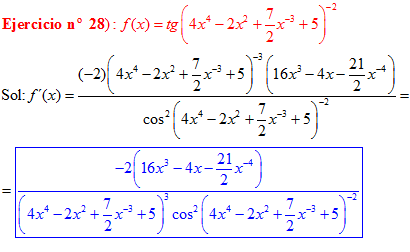
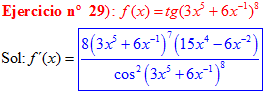
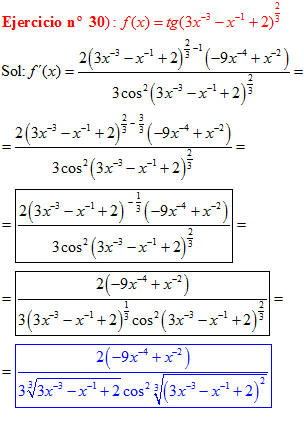
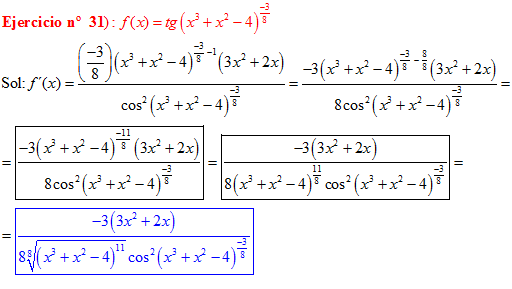
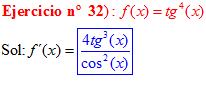
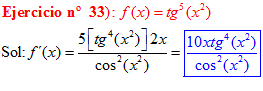
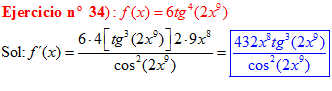
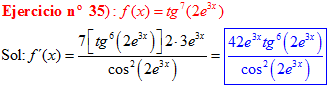
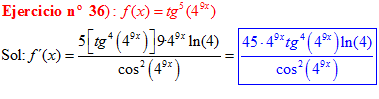
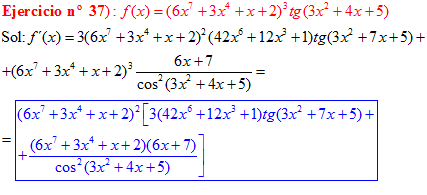
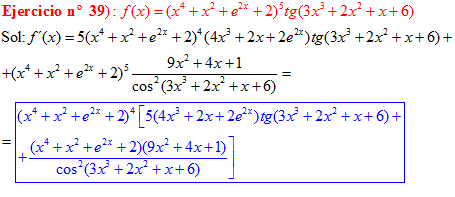
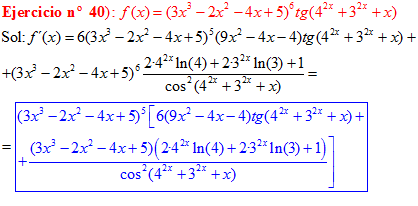
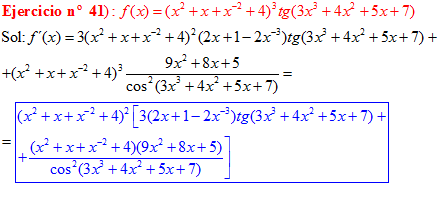
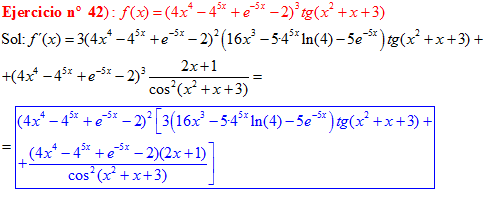
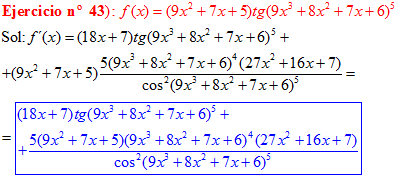
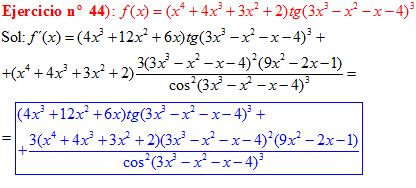
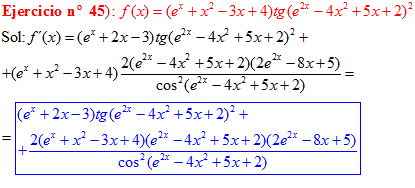
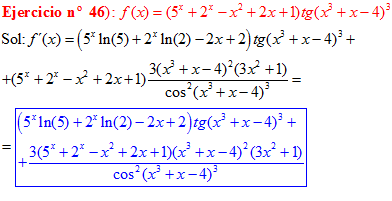
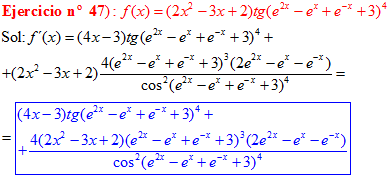
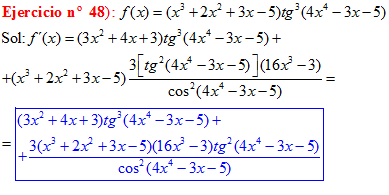
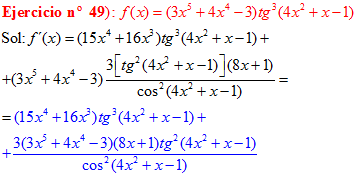
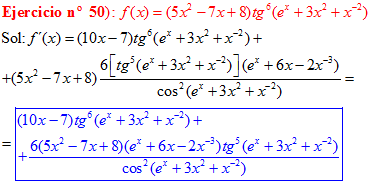
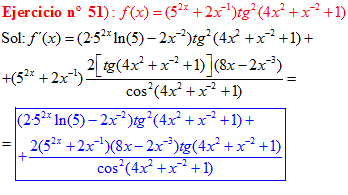
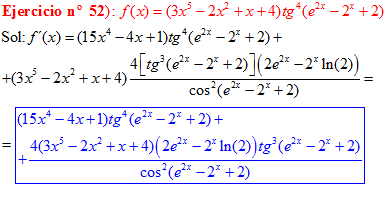
❊❊❊❊❊ FIN FÓRMULA 9 ❊❊❊❊❊
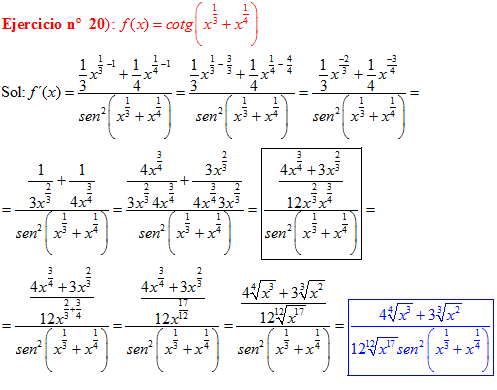
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COTANGENTE
|
FÓRMULA 10 compuesta
LA DERIVADA DE LA COTANGENTE DE x es igual a menos la unidad dividida por el seno cuadrado de x |
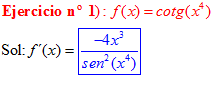
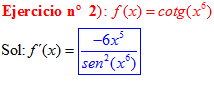
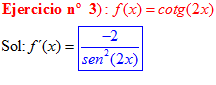
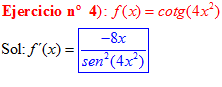
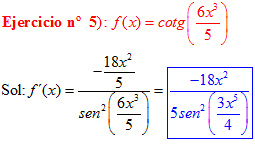
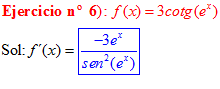
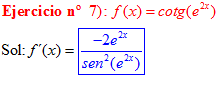
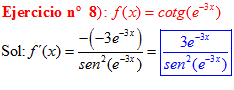

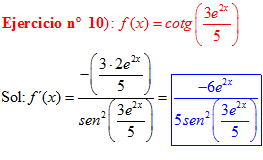
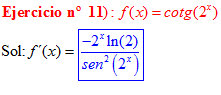
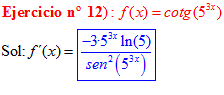
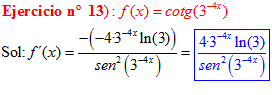

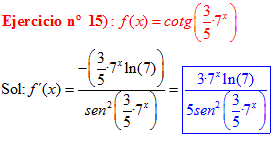
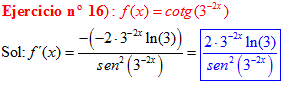
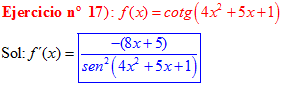
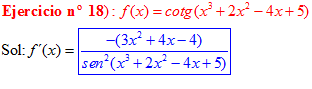
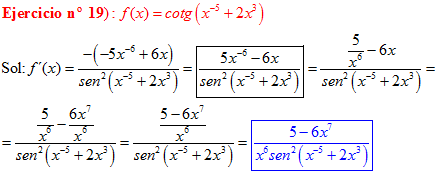
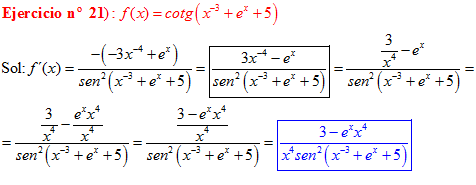
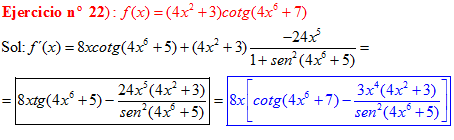
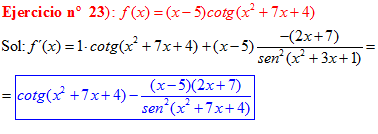
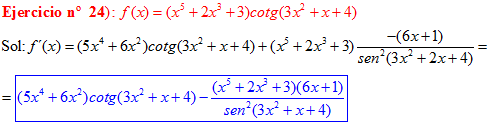
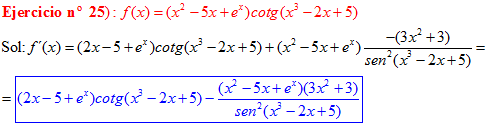
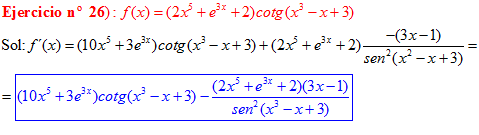
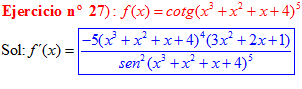
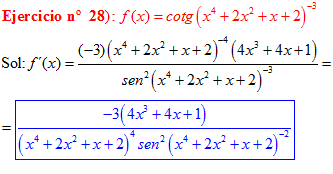
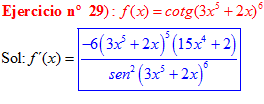
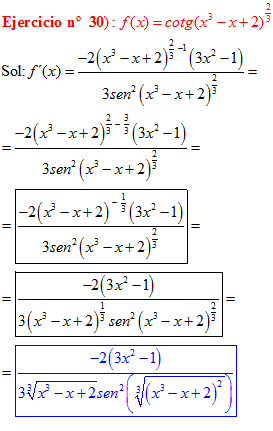
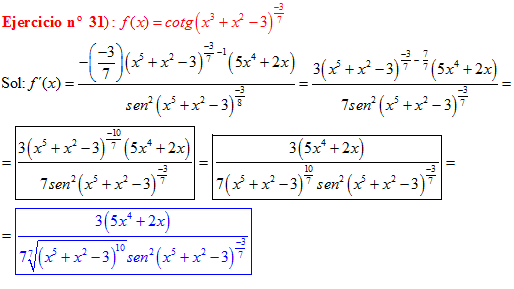

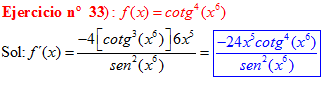
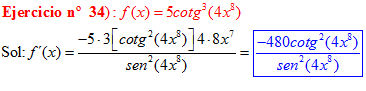
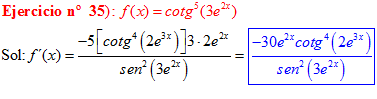
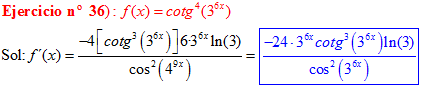
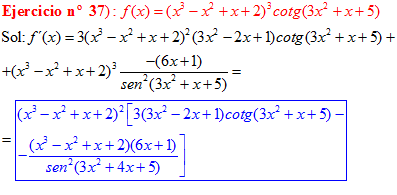
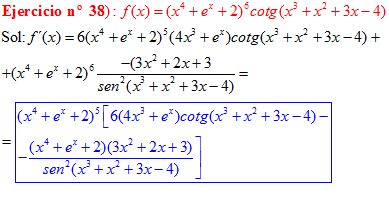
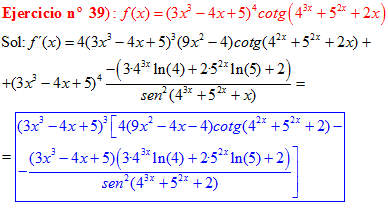
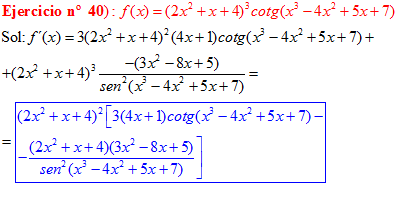
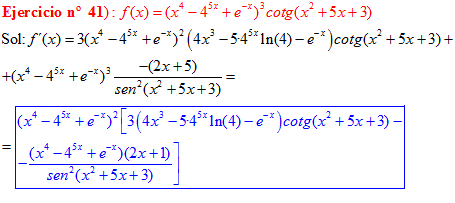


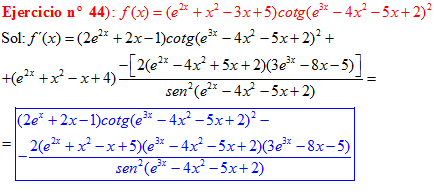
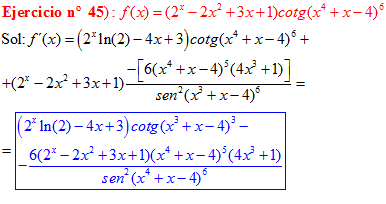
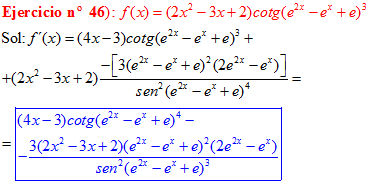
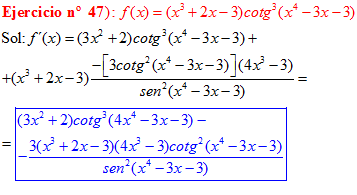

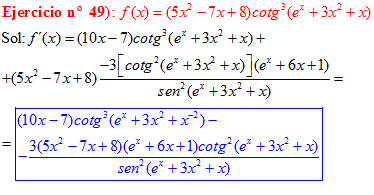
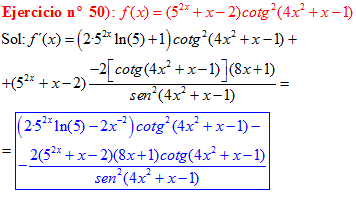
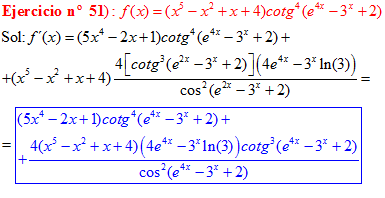
❊❊❊❊❊ FIN FÓRMULA 10 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA SECANTE
|
FÓRMULA 11 compuesta
LA DERIVADA DEL SECANTE DE x es igual a secante de x por tangente de x |

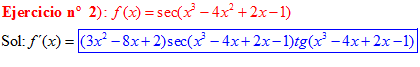
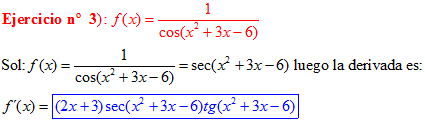

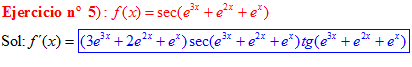
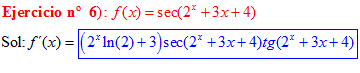
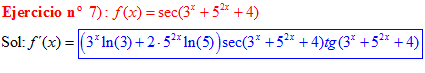
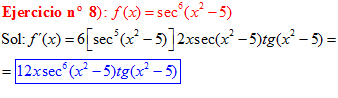
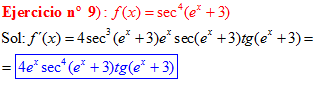
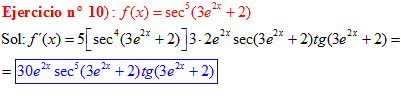
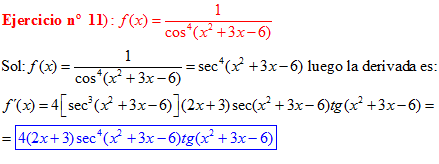
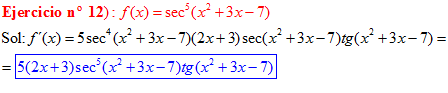
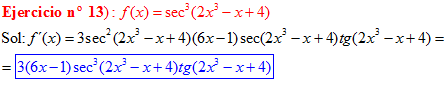
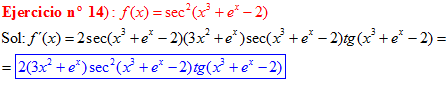
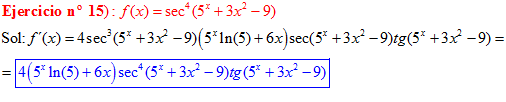
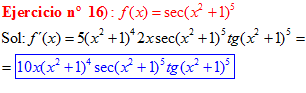
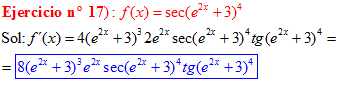
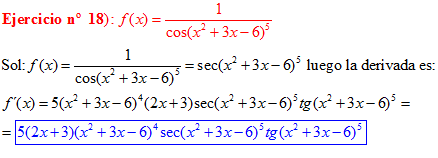
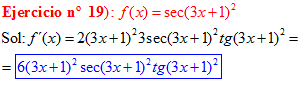
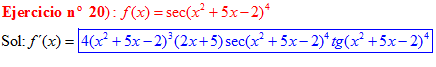
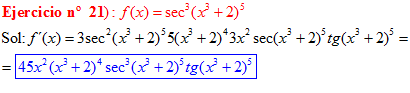
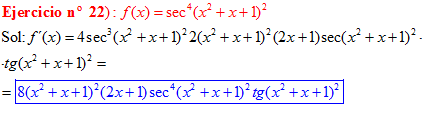
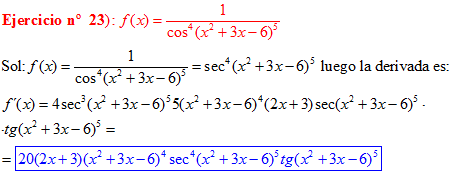
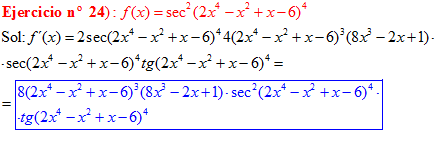
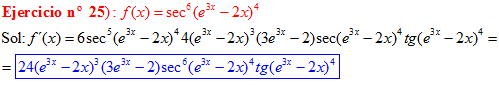
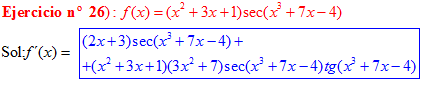
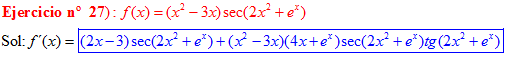
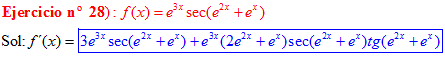
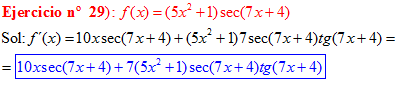
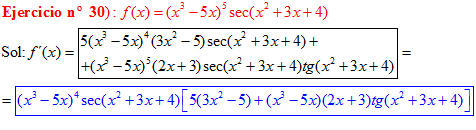
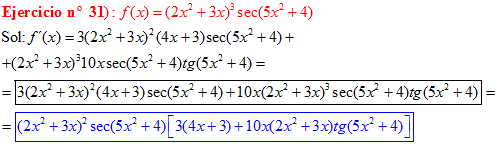
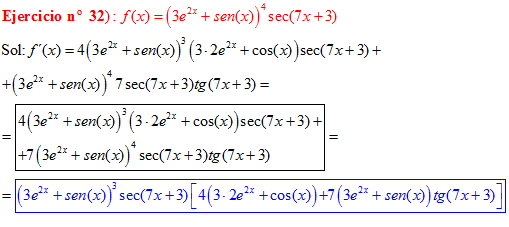
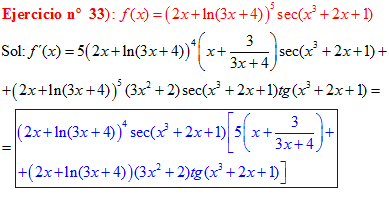
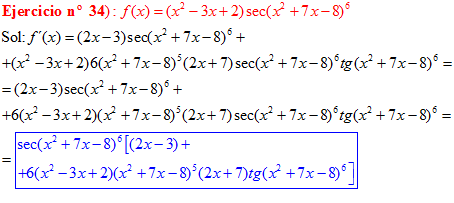
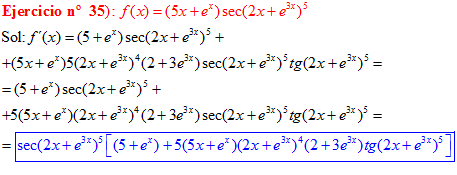
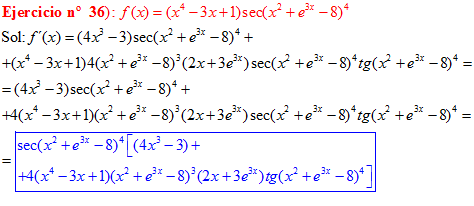
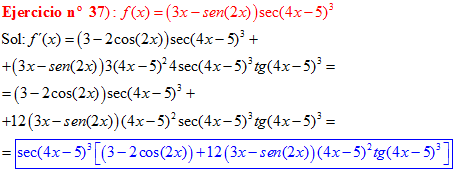
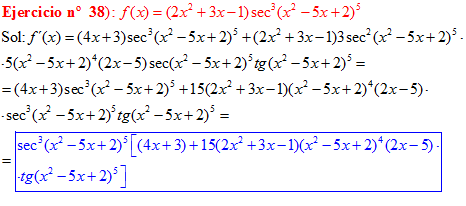
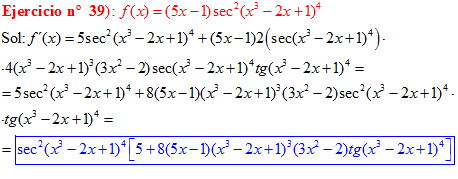
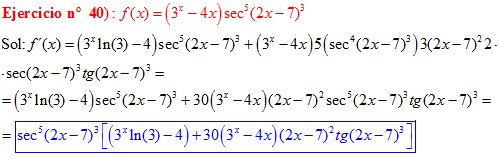

❊❊❊❊❊ FIN FÓRMULA 11 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COSECANTE
|
FÓRMULA 12 compuesta
LA DERIVADA DEL COSECANTE DE x es igual a menos cosecante de x por tangente de x |
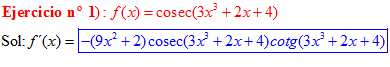

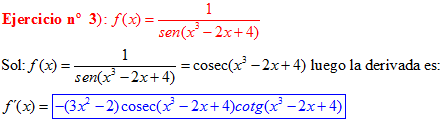
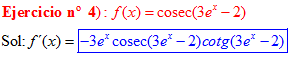
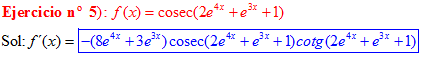
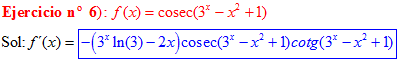
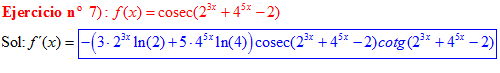
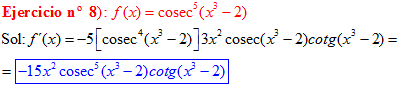
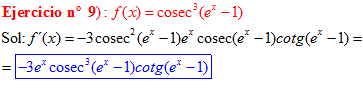
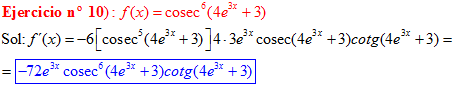
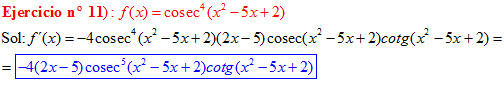
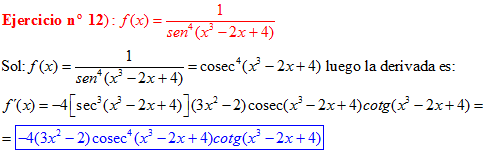
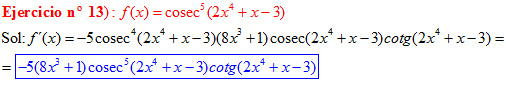
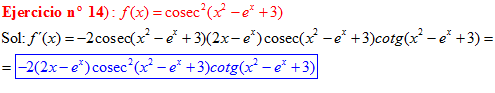
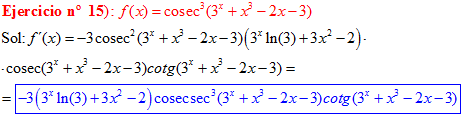
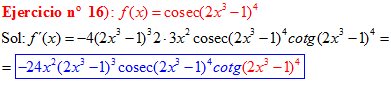
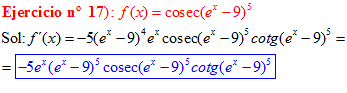
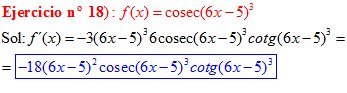
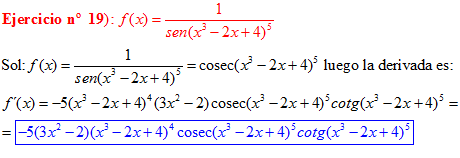
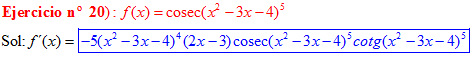
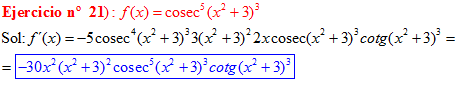
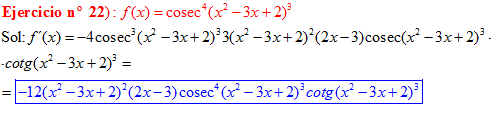

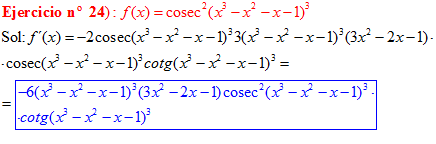
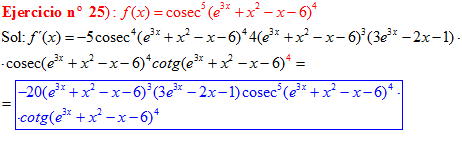
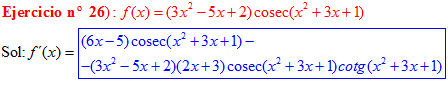
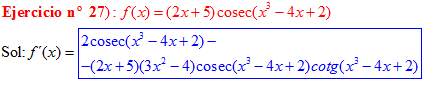

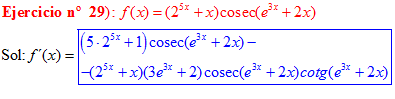
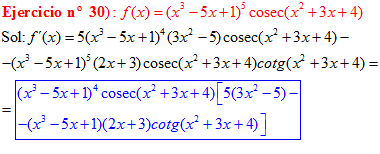
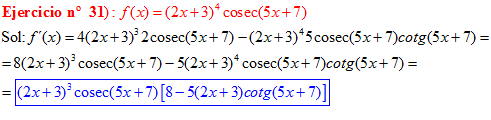
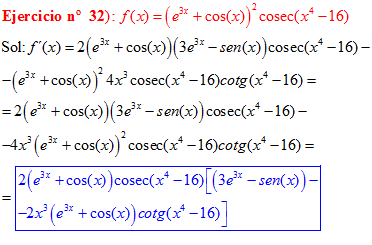

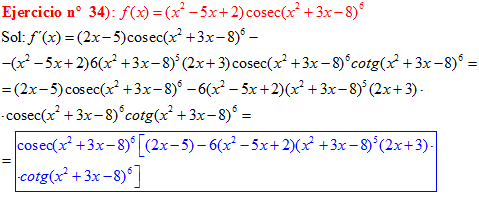
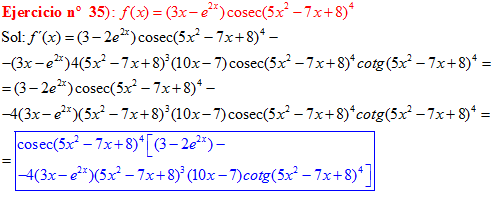
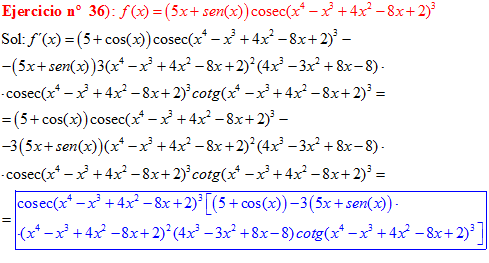
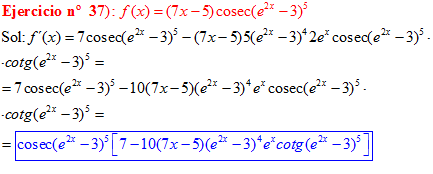
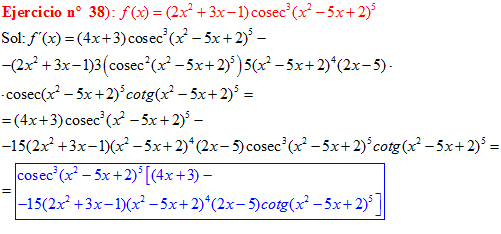
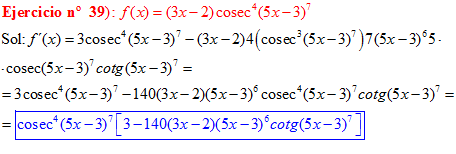
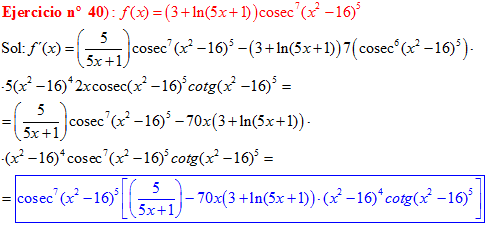
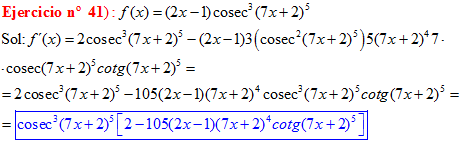
❊❊❊❊❊ FIN FÓRMULA 12 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO SENO
|
FÓRMULA 13 compuesta
LA DERIVADA DEL ARCO SENO DE UNA FUNCIÓN DE x es igual a la derivada de la función de x dividida entre la raíz cuadrada de la unidad menos la función al cuadrado |
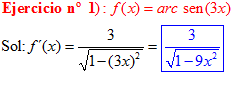
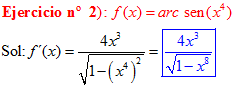
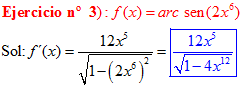
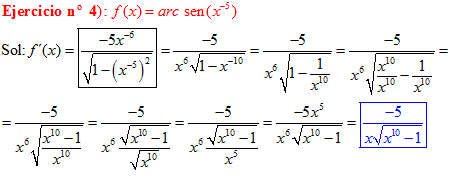
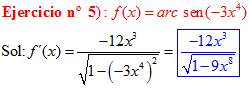
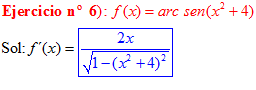
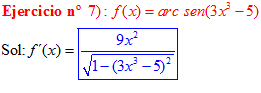
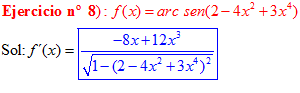
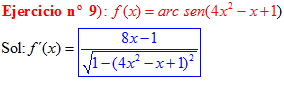
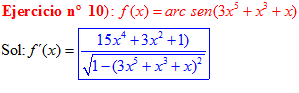
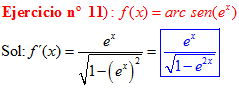
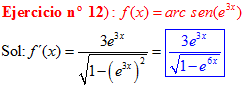
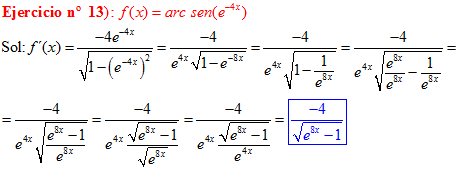
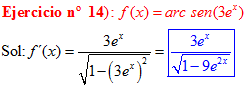
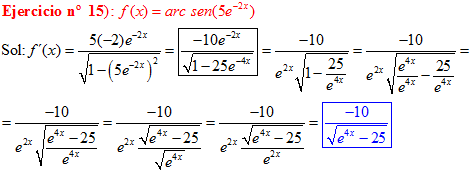
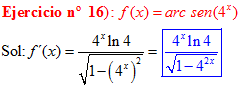
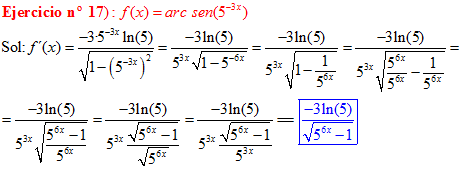
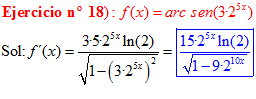
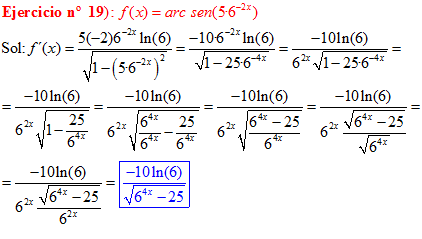
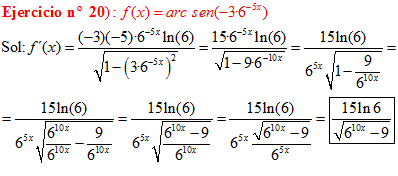

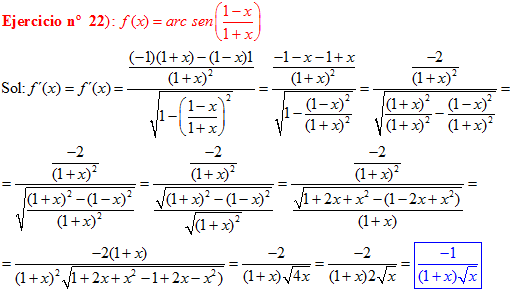
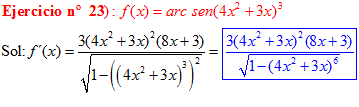
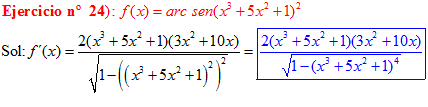
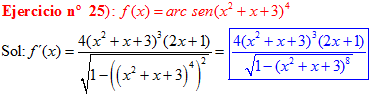
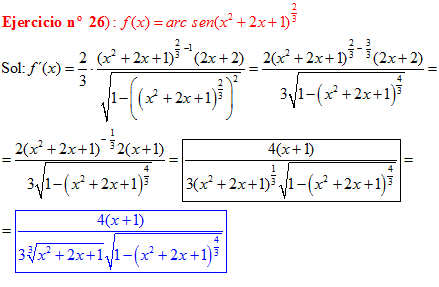
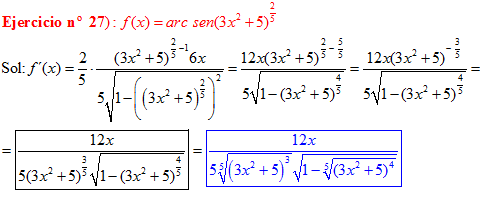
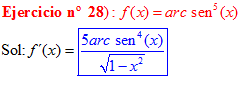
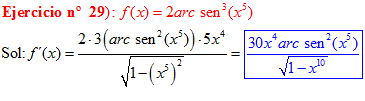
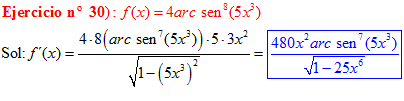
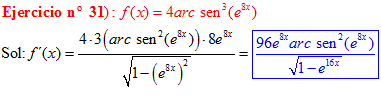
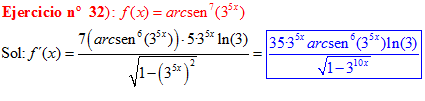
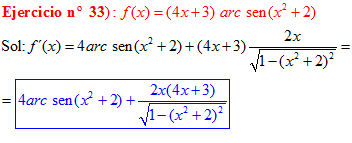
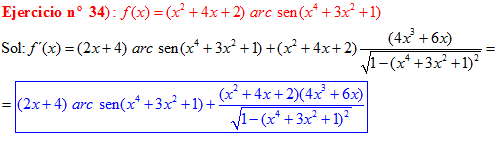
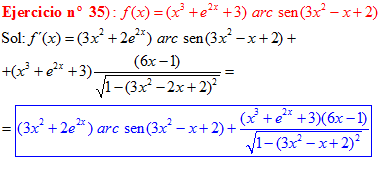
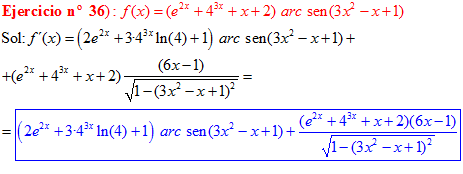
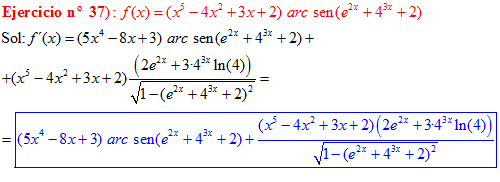
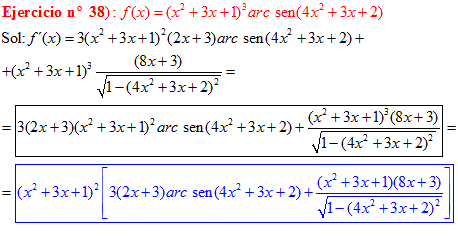
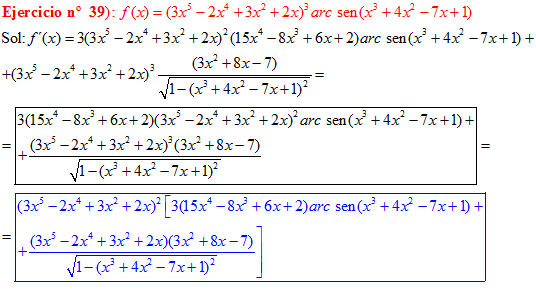


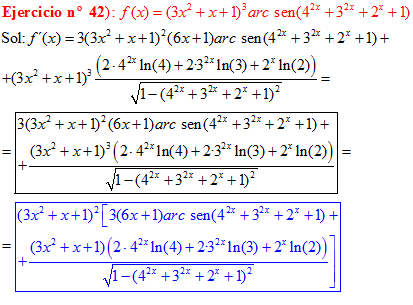
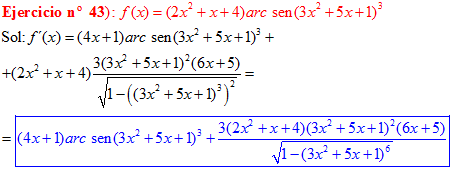
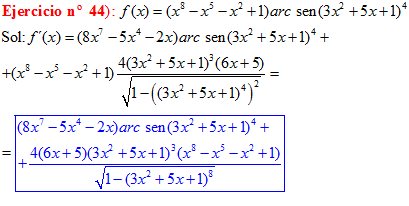
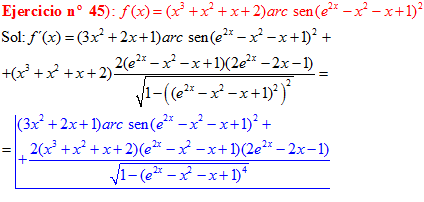
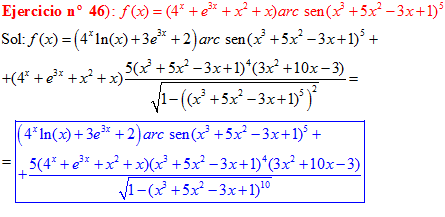
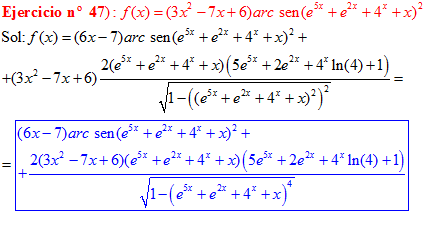
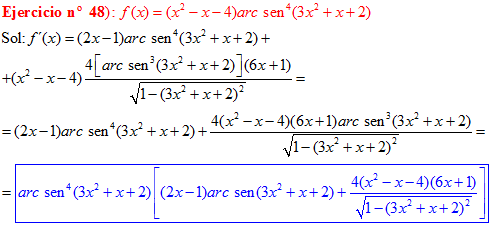
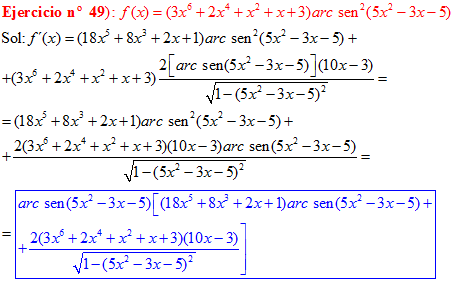


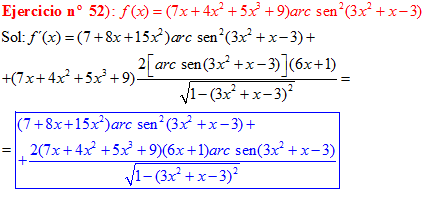
❊❊❊❊❊ FIN FÓRMULA 13 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COSENO
|
FÓRMULA 14 compuesta
LA DERIVADA DEL ARCO COSENO DE UNA FUNCIÓN DE x es igual a menos la derivada de la función de x dividida entre la raíz cuadrada de la unidad menos la función al cuadrado |
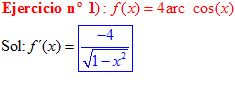
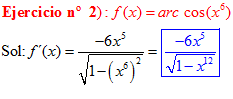
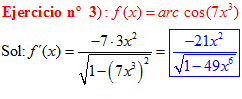
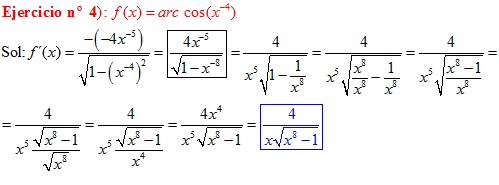
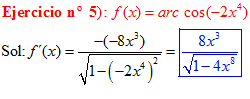
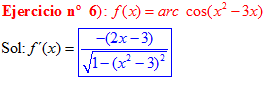
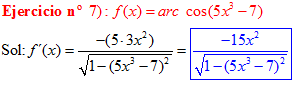
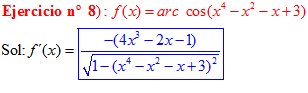
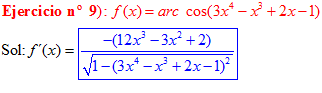
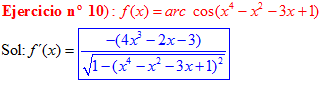

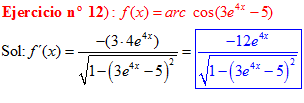
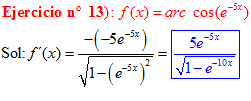
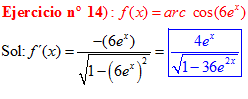
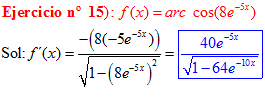
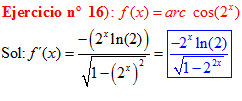
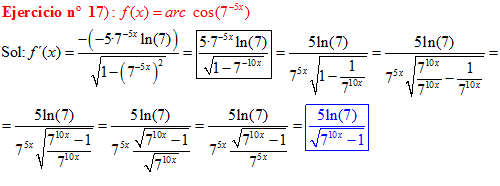
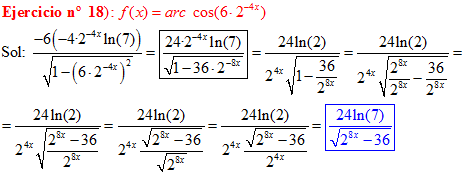
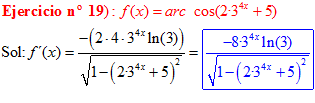
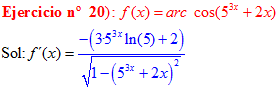
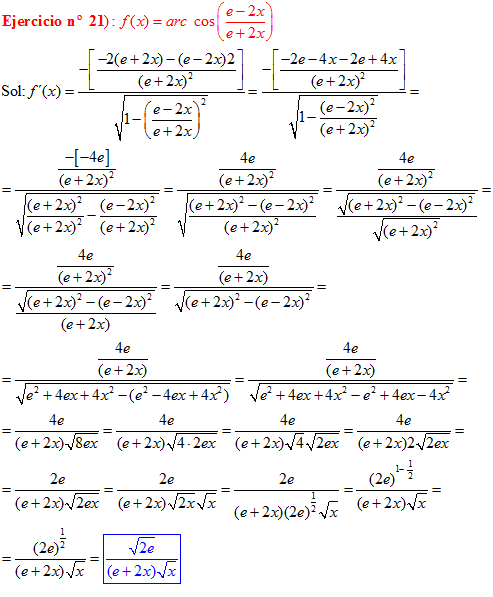

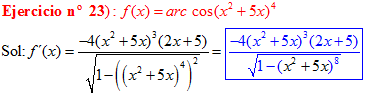
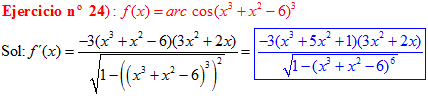
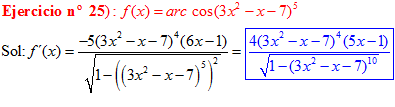
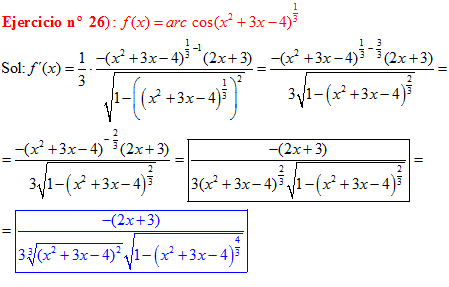
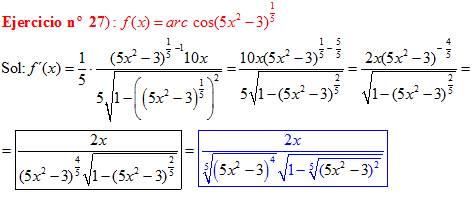
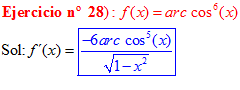
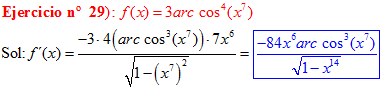
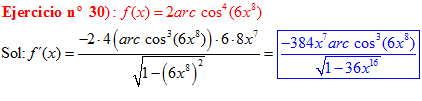
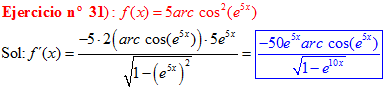
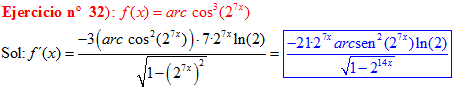
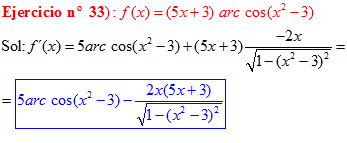
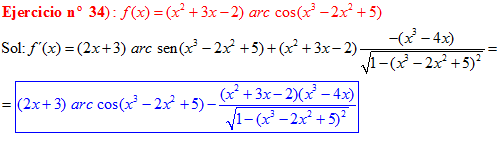
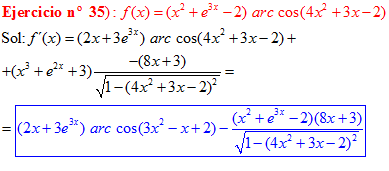
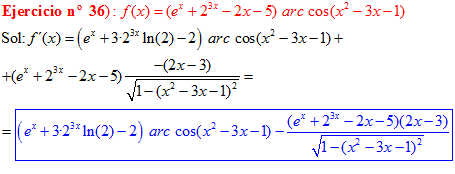
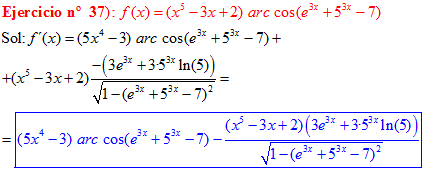
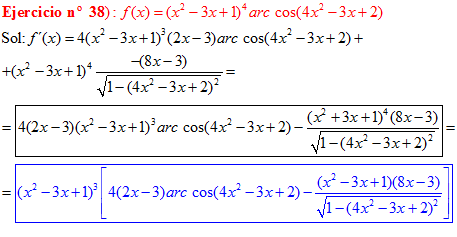
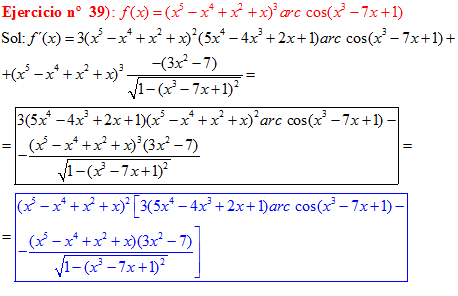
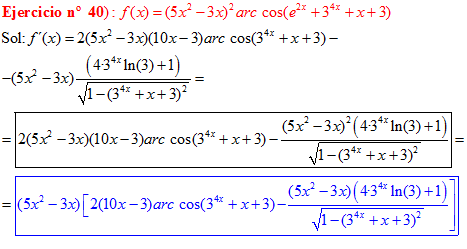

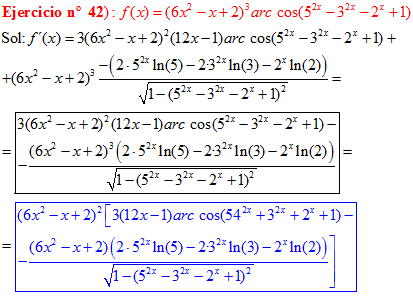
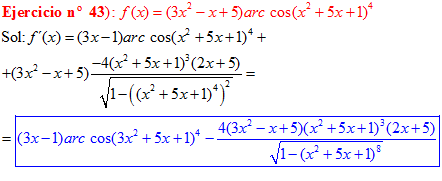
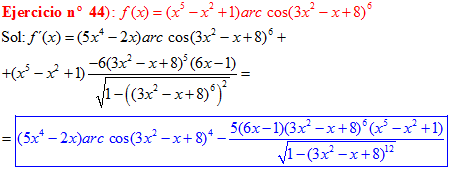
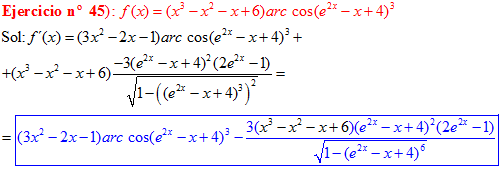
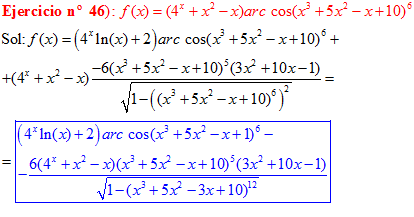
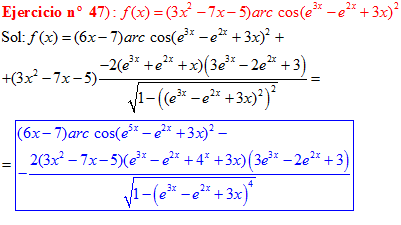
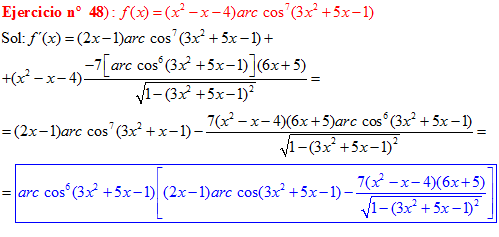
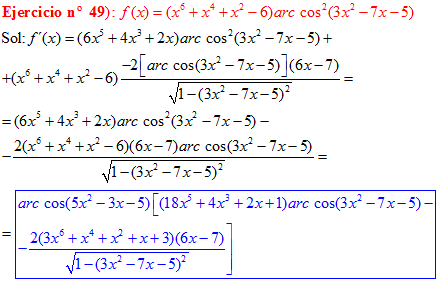

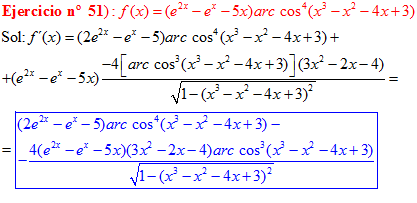
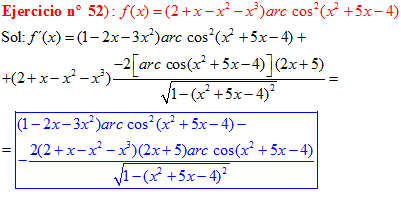
❊❊❊❊❊ FIN FÓRMULA 14 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO TANGENTE
|
FÓRMULA 15 compuesta
LA DERIVADA DEL ARCO TANGENTE DE UNA FUNCIÓN DE x es igual a la derivada de la función de x dividida entre la unidad mas la función al cuadrado |

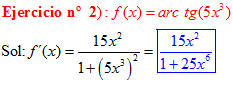


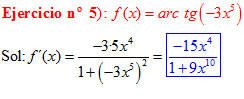
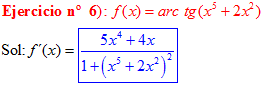
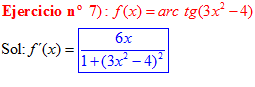
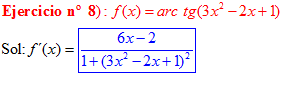
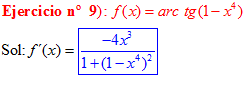
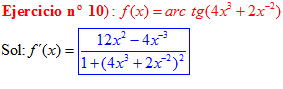
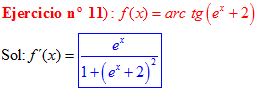

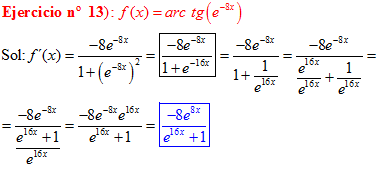
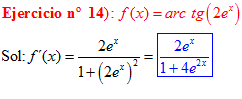
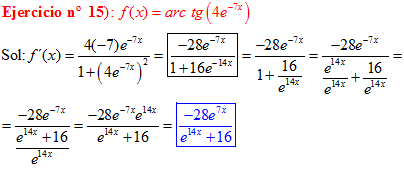
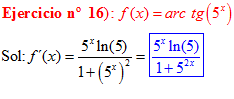
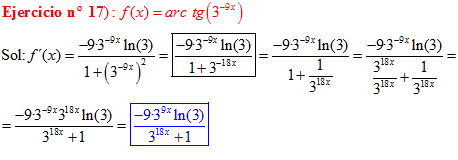
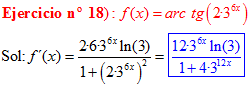
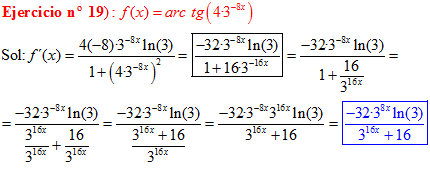
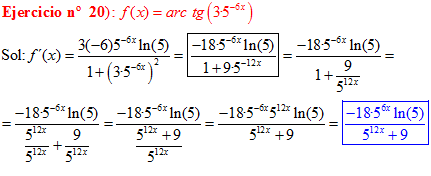
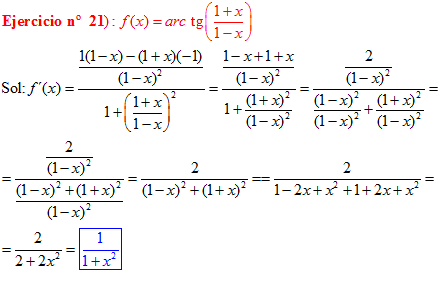
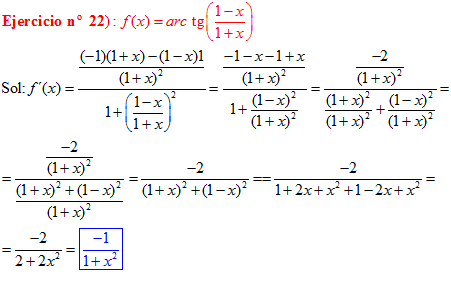
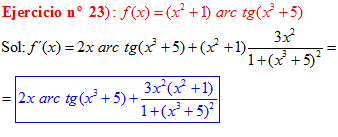
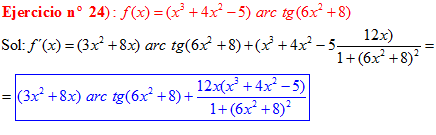
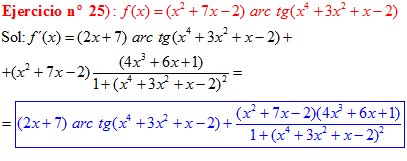
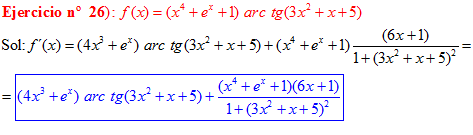
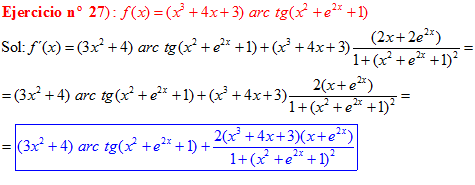
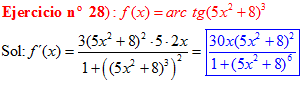
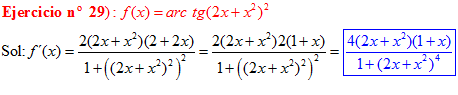
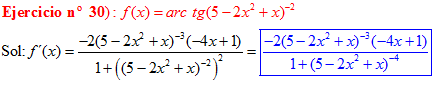
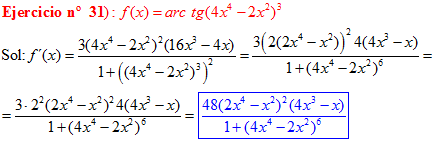
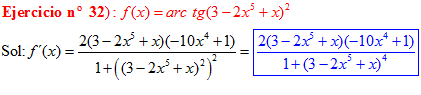
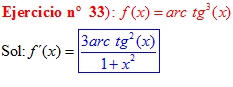
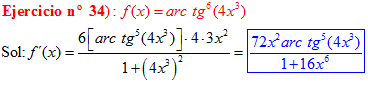
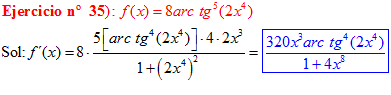
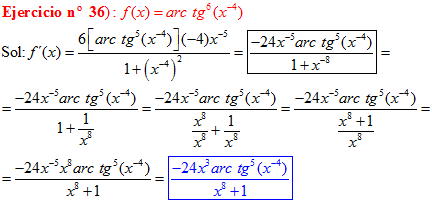
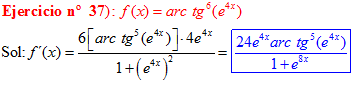
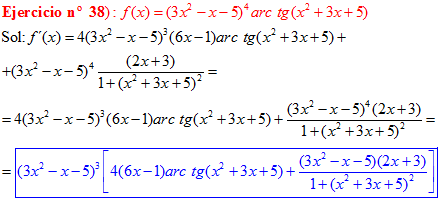

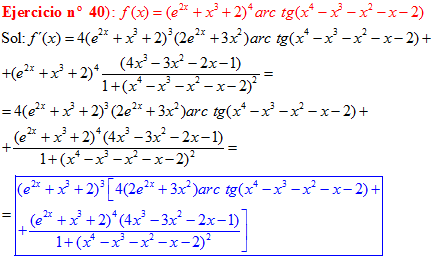

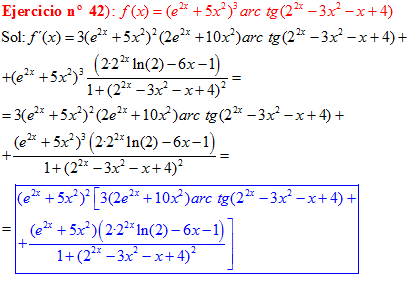
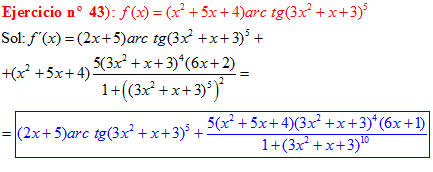
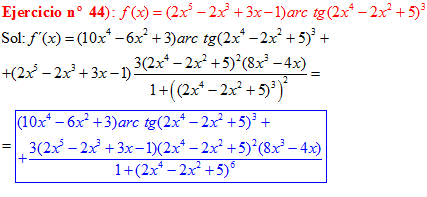
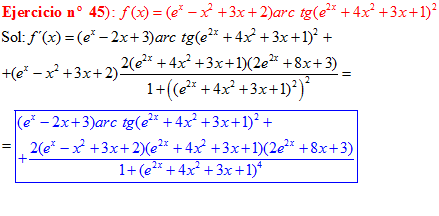
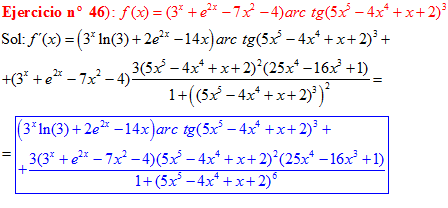
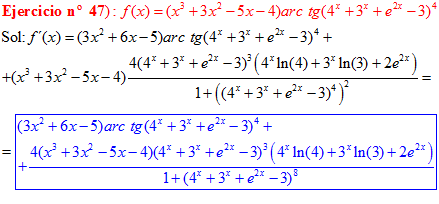
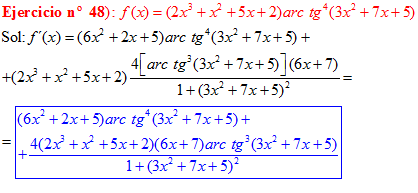
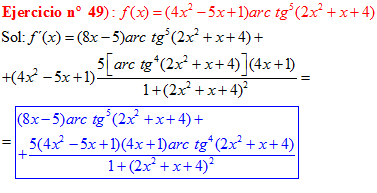
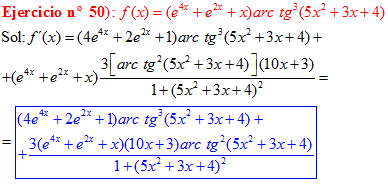
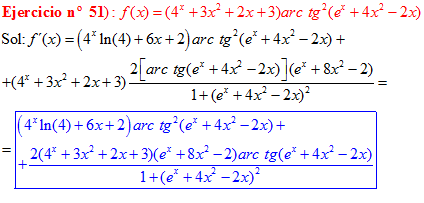
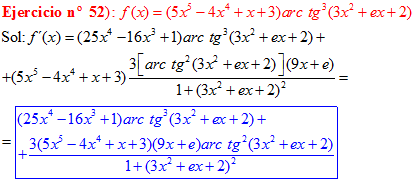
❊❊❊❊❊ FIN FÓRMULA 15 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COTANGENTE
|
FÓRMULA 16 compuesta
LA DERIVADA DEL ARCO COTANGENTE DE UNA FUNCIÓN DE x es igual a menos la derivada de la función de x dividida entre la unidad mas la función al cuadrado |

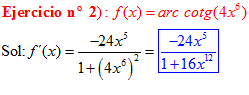
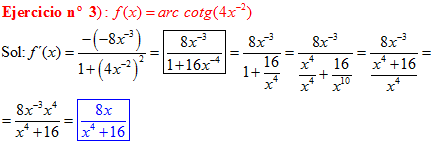
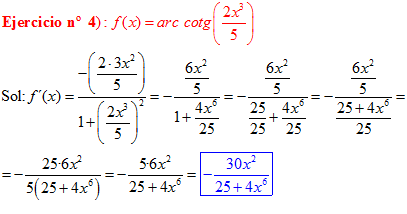
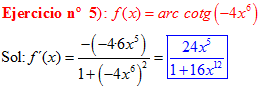
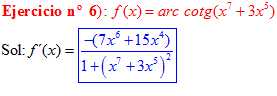
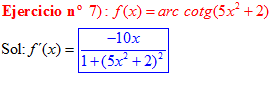
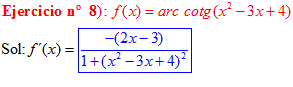
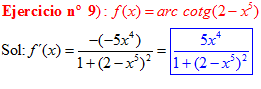
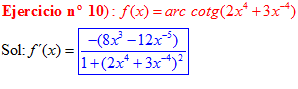
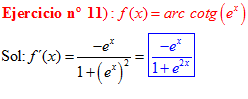
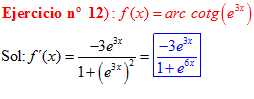
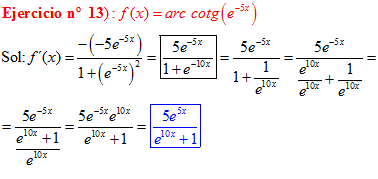
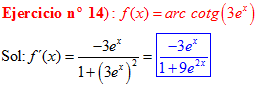
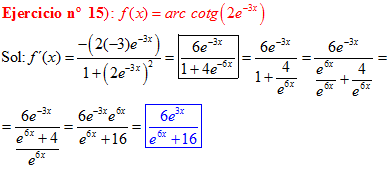
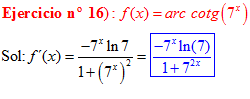
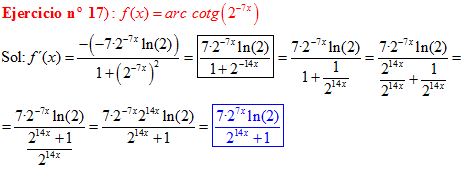
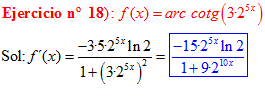
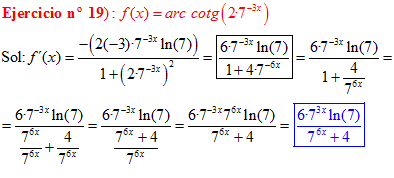
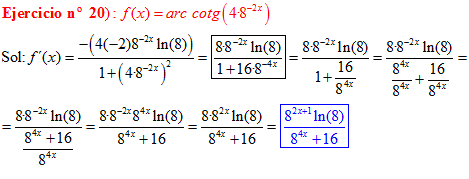
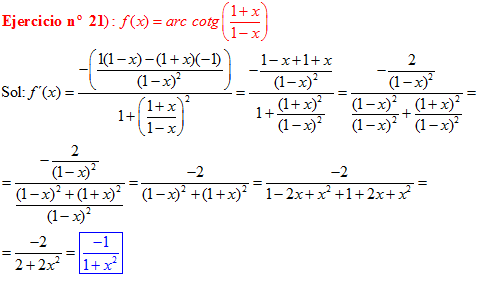
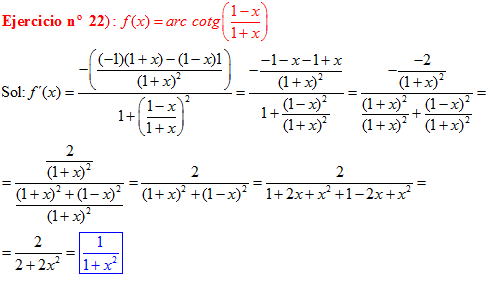

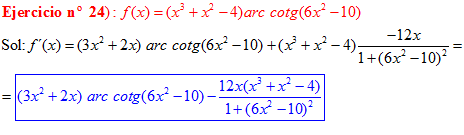
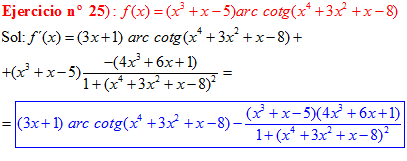
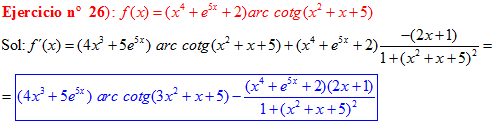
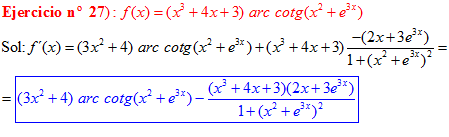
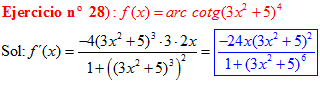
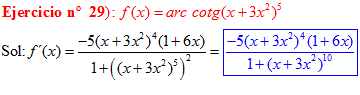
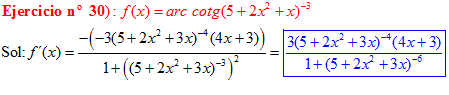
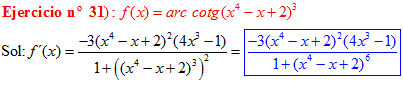
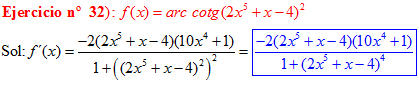
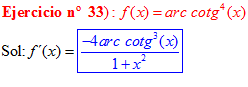
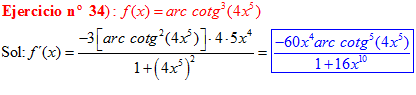
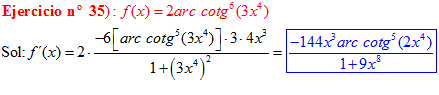
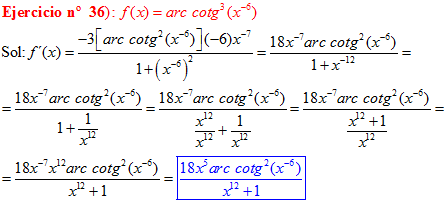
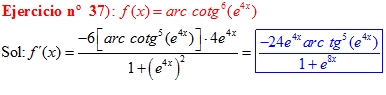
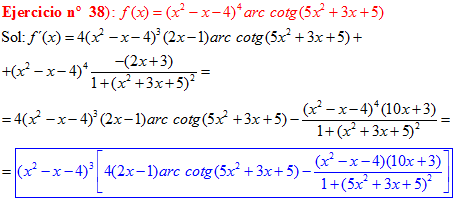
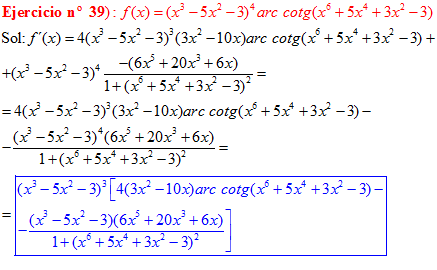
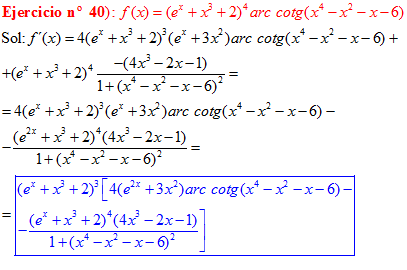
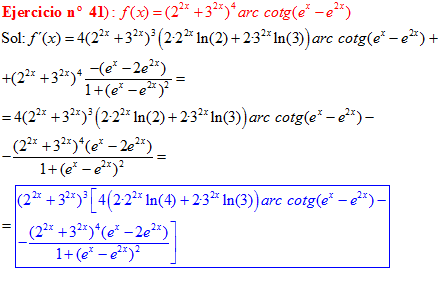
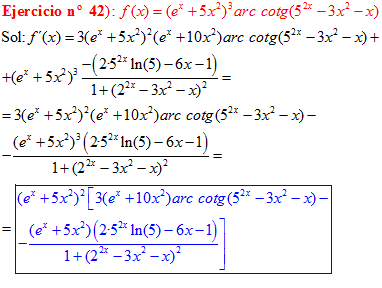
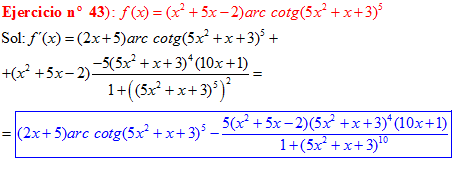
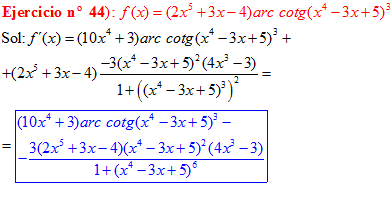
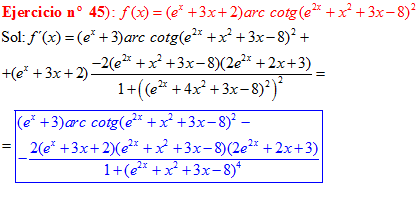
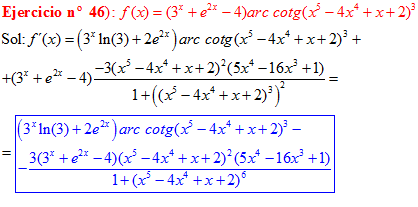
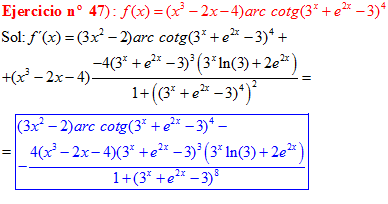
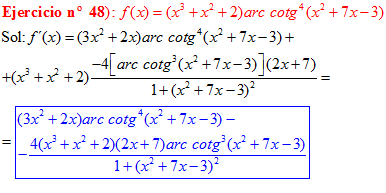

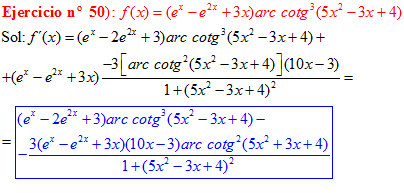
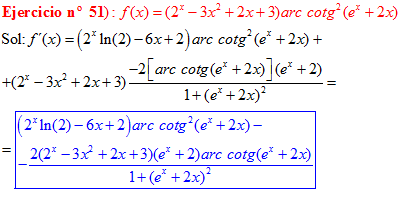
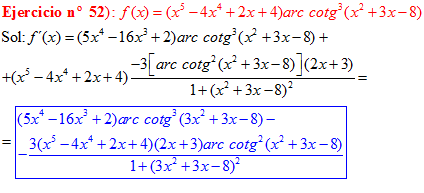
❊❊❊❊❊ FIN FÓRMULA 16 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO SECANTE
|
FÓRMULA 17 compuesta
LA DERIVADA DEL ARCO SECANTE DE x es igual a la unidad dividida entre x por la raíz cuadrada de x al cuadrado menos uno |
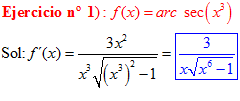

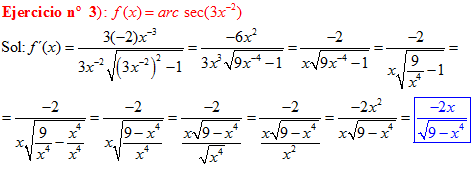
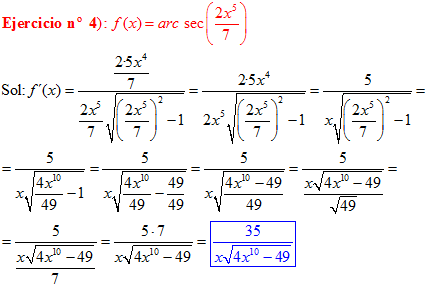
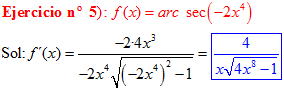
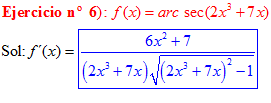
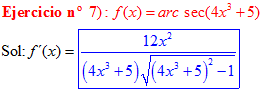
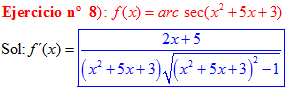
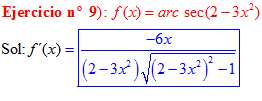
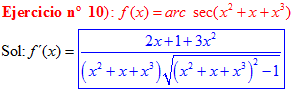

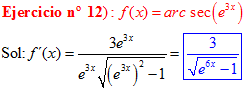
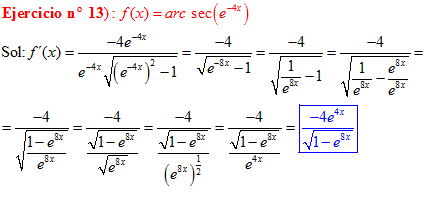
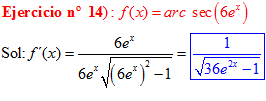
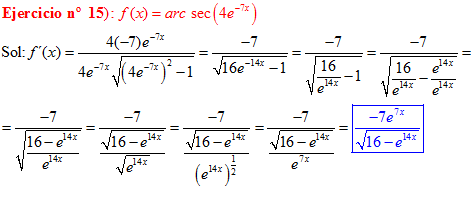
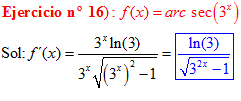

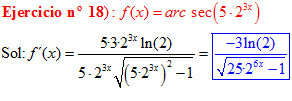
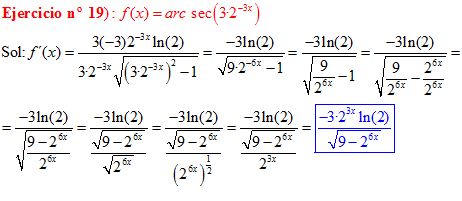
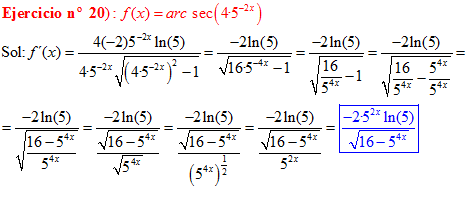
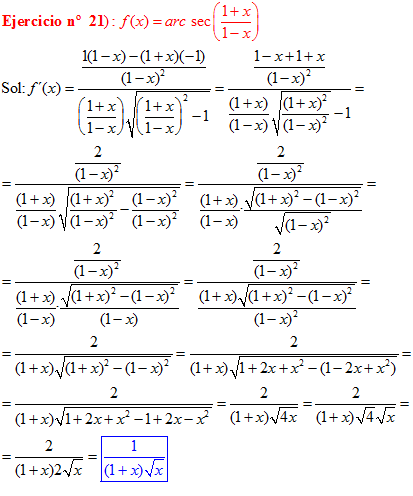
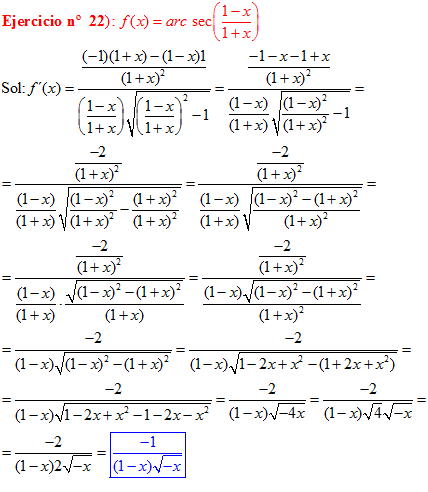
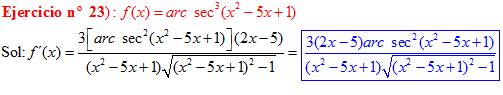
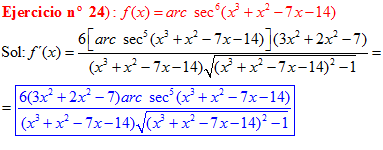
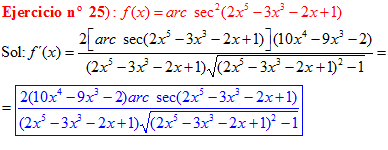
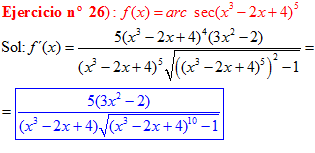
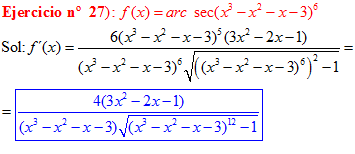
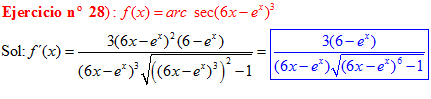
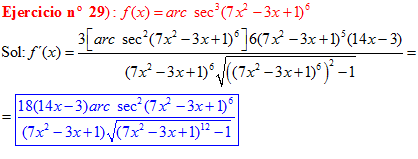
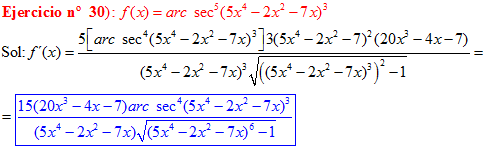
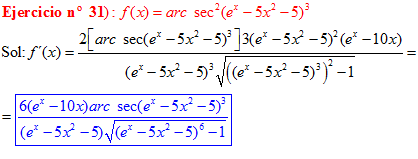
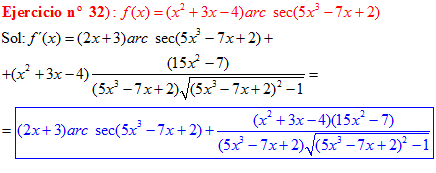
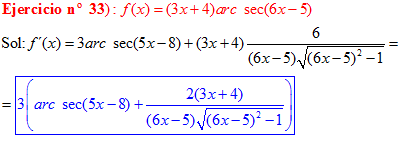
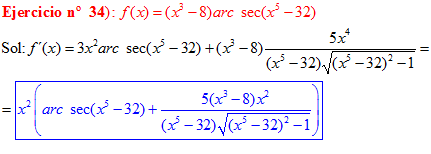
❊❊❊❊❊ FIN FÓRMULA 17 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COSECANTE
|
FÓRMULA 18 compuesta
LA DERIVADA DEL ARCO COSECANTE DE x es igual a menos la unidad dividida entre x por la raíz cuadrada de x al cuadrado menos uno |
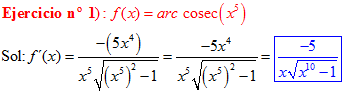

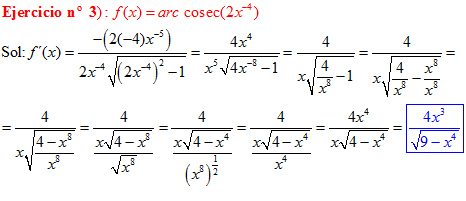
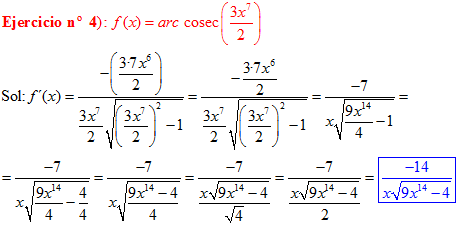
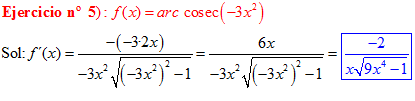
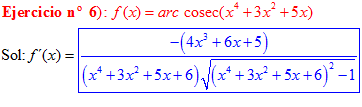
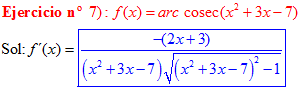

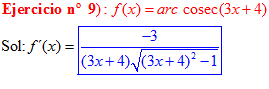
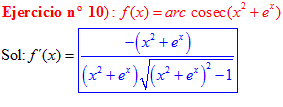
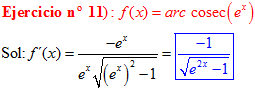
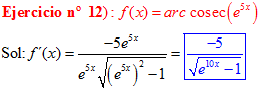
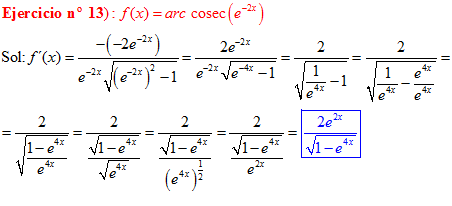
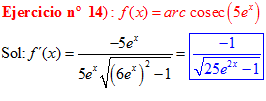
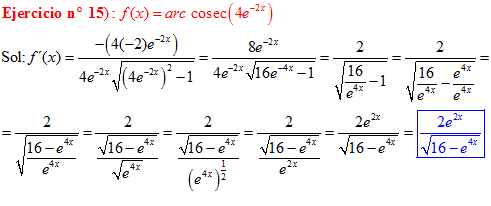
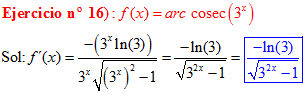
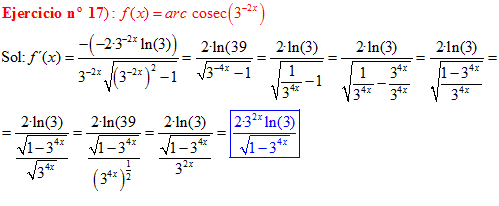
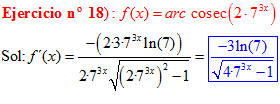
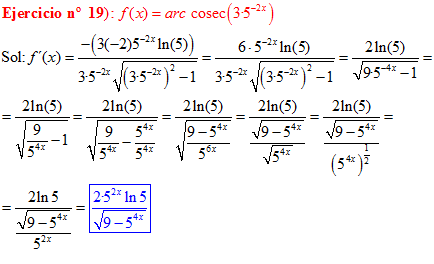
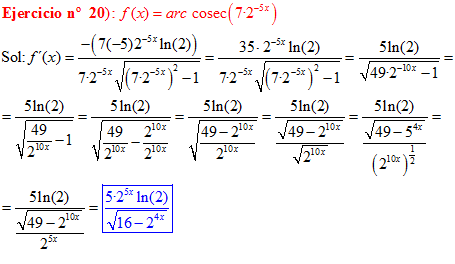
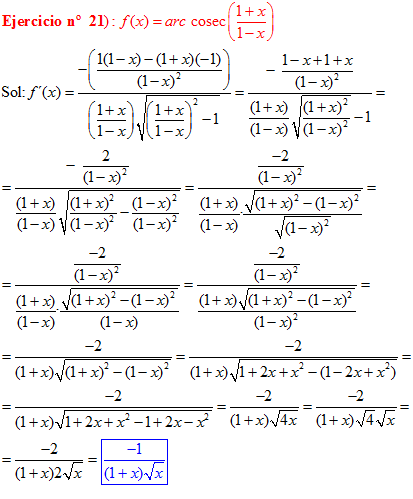
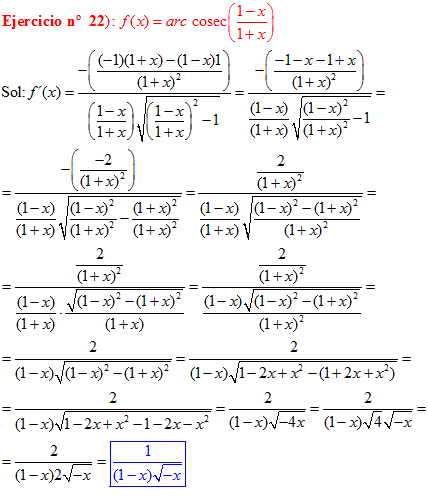
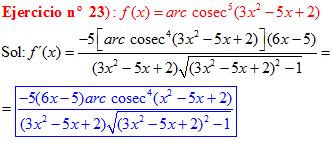
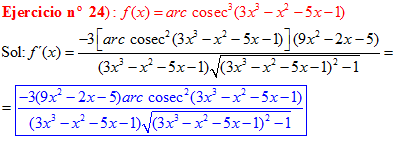
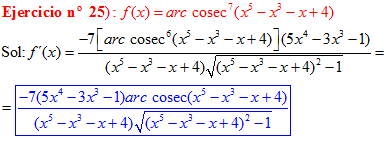
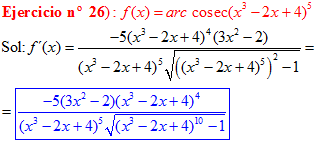
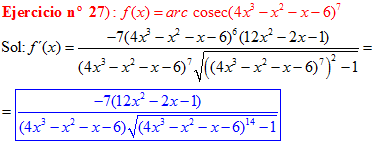
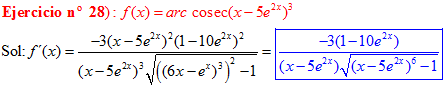
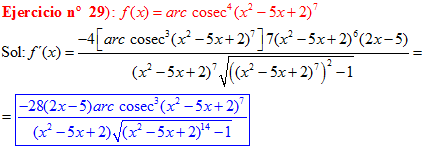

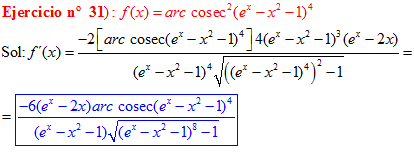
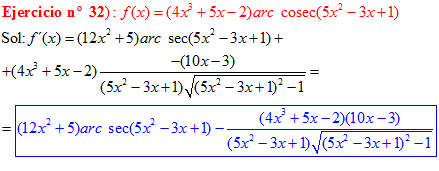
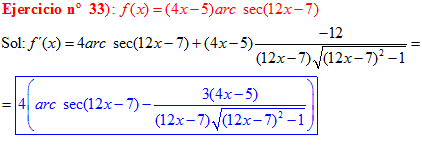
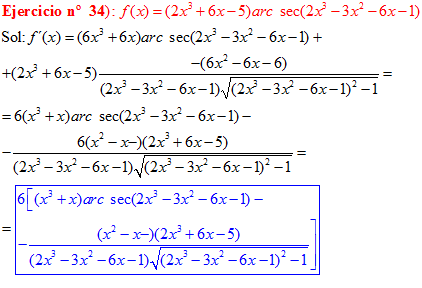
❊❊❊❊❊ FIN FÓRMULA 18 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
SENO HIPÉRBOLICO
|
FÓRMULA 19 compuesta
LA DERIVADA DEL SENO HIPERBÓLICO DE una función de x es igual a la derivada de dicha función por el coseno hiperbólico de la función |
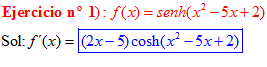
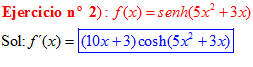
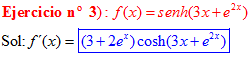
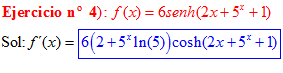
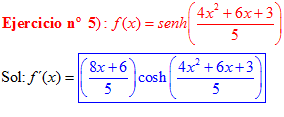
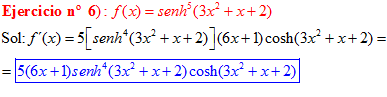
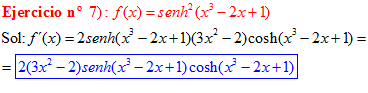
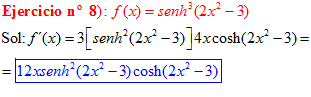
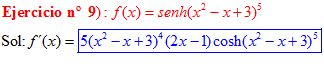
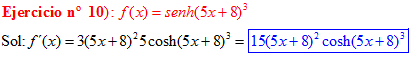

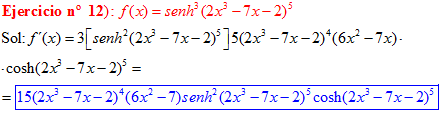
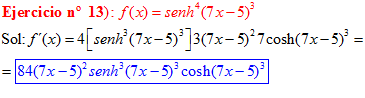
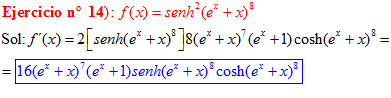
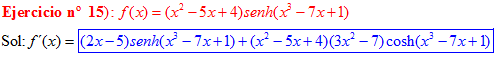
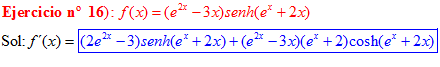
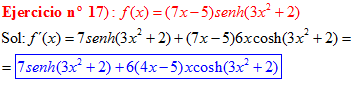
❊❊❊❊❊ FIN FÓRMULA 19 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
COSENO HIPÉRBOLICO
|
FÓRMULA 20 compuesta
LA DERIVADA DEL COSENO HIPERBÓLICO DE una función de x es igual a la derivada de dicha función por el seno hiperbólico de la función |
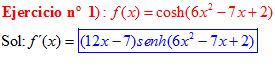
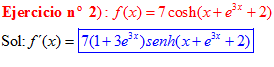
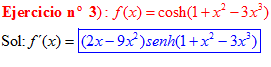
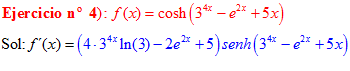
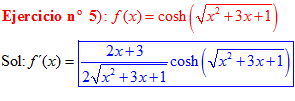
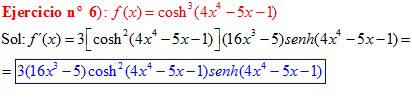
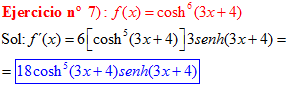
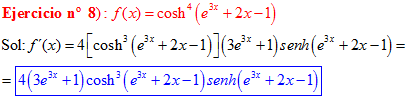
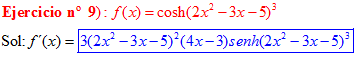
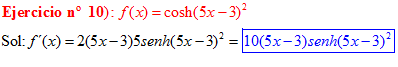
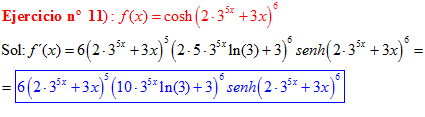
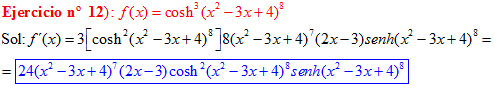

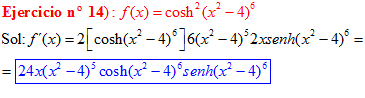
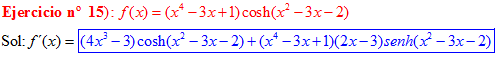
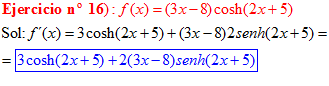

❊❊❊❊❊ FIN FÓRMULA 20 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
TANGENTE HIPÉRBOLICA
|
FÓRMULA 21 compuesta
LA DERIVADA DE LA TANGENTE HIPERBÓLICA DE una función de x es igual a la derivada de dicha función por la secante hiperbólica al cuadrado de la función |
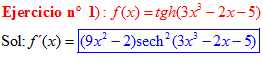
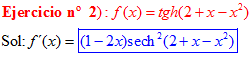
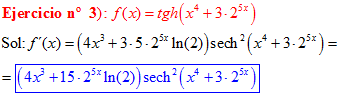
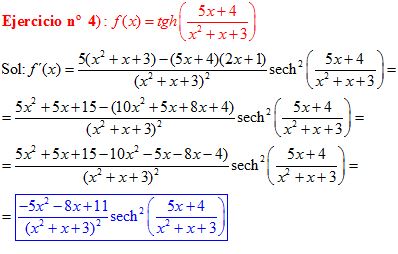
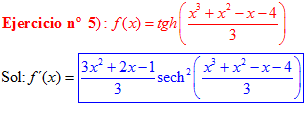
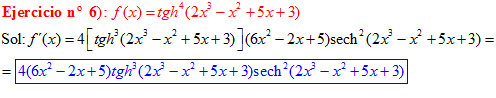
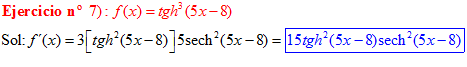
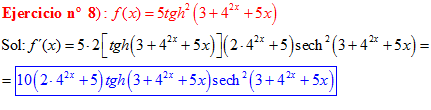
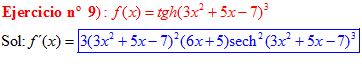
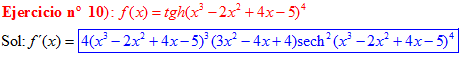
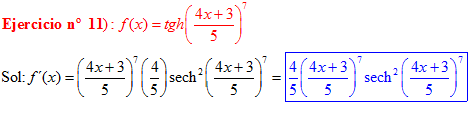
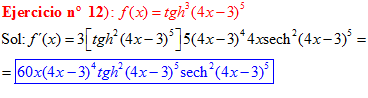
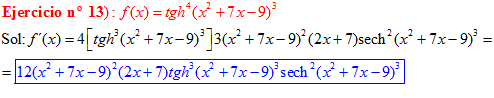
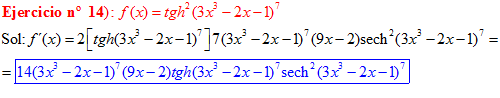
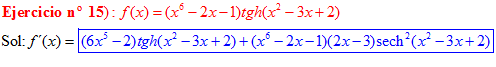
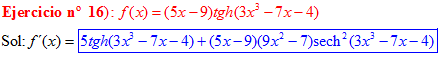
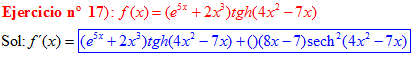
❊❊❊❊❊ FIN FÓRMULA 21 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
COTANGENTE HIPÉRBOLICA
|
FÓRMULA 22 compuesta
LA DERIVADA DE LA COTANGENTE HIPERBÓLICA DE una función de x es igual a menos la derivada de dicha función por la cosecante hiperbólica al cuadrado de la función |
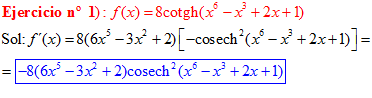
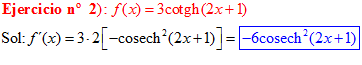
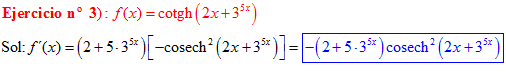
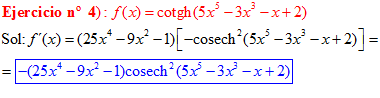
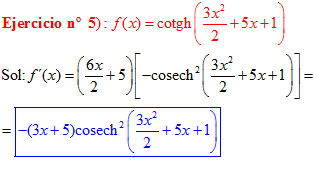
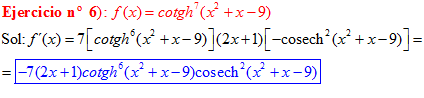
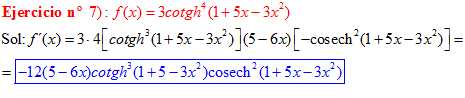
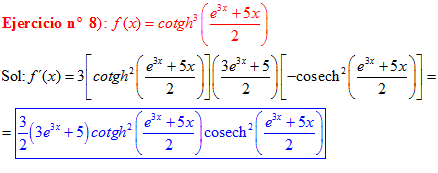
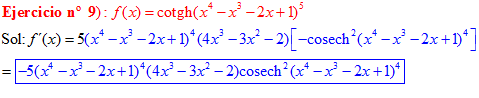
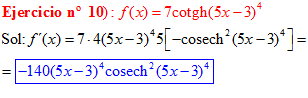
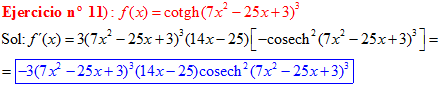
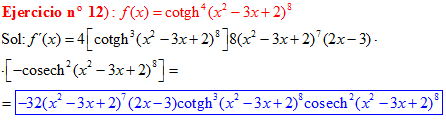
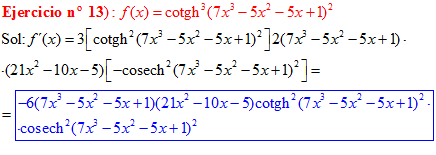
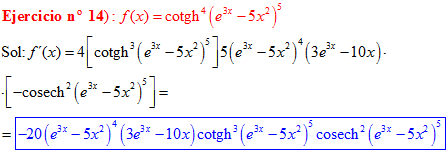
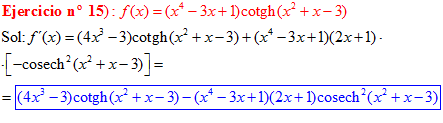
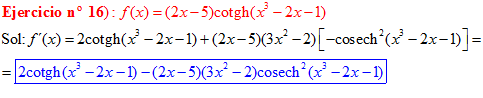
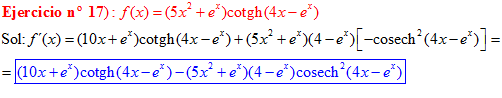
❊❊❊❊❊ FIN FÓRMULA 22 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
SECANTE HIPÉRBOLICA
|
FÓRMULA 23 compuesta
LA DERIVADA DE LA SECANTE HIPERBÓLICA DE una función de x es igual a menos la derivada de dicha función por la secante hiperbólica de la función y por la tangente hiperbólica de la misma |
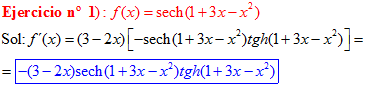
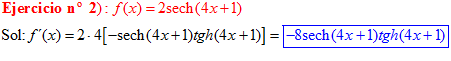
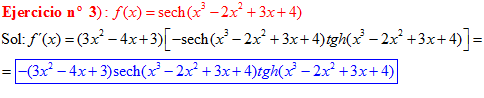
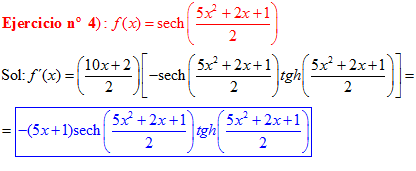
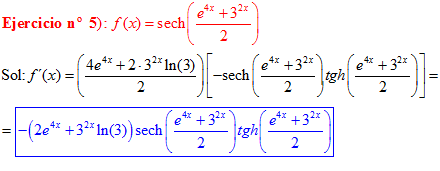
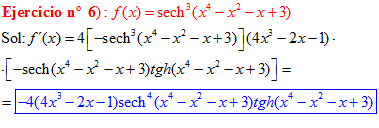
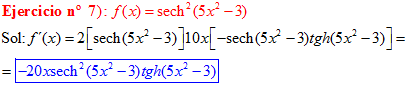
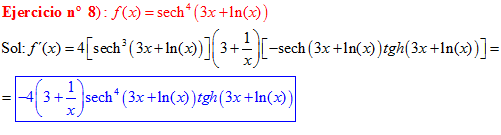

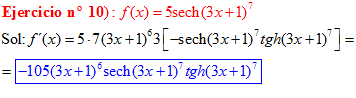
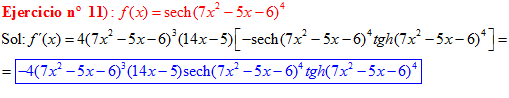
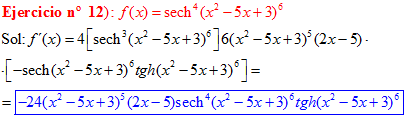
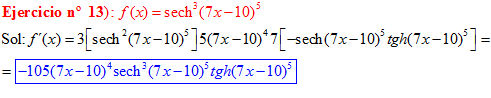
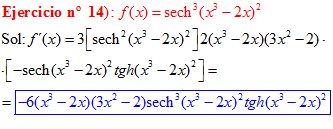
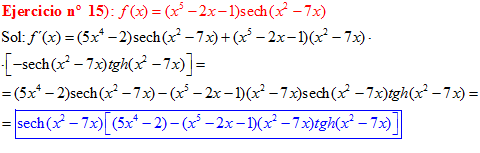
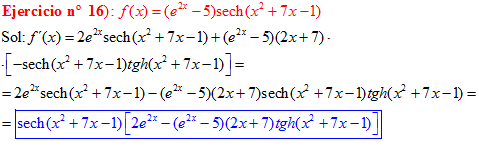
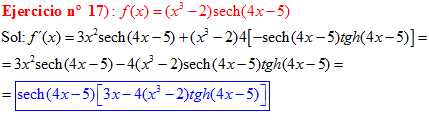
❊❊❊❊❊ FIN FÓRMULA 23 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
COSECANTE HIPÉRBOLICA
|
FÓRMULA 24 compuesta
LA DERIVADA DE LA COSECANTE HIPERBÓLICA DE una función de x es igual a menos la derivada de dicha función por la cosecante hiperbólica de la función y por la cotangente hiperbólica de la misma |
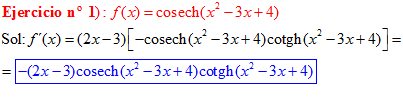
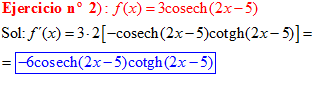
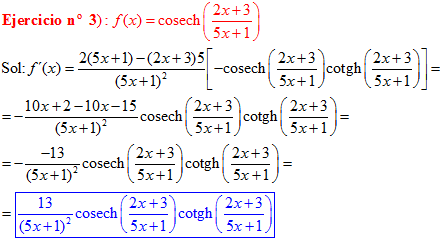
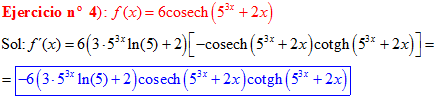
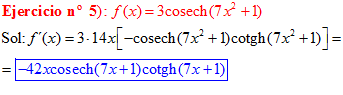



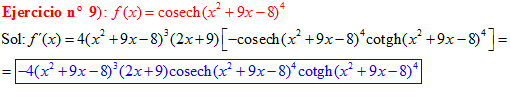
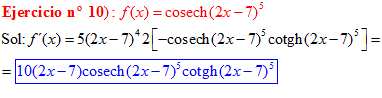
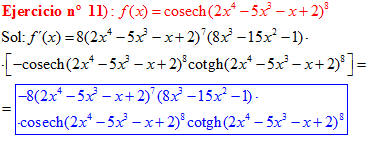
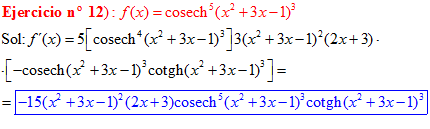
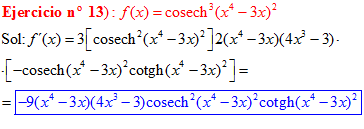
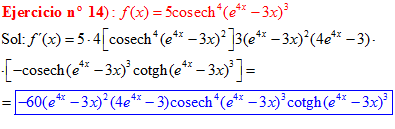
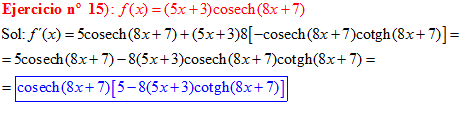
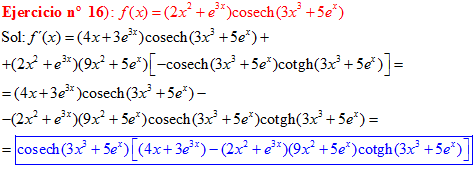
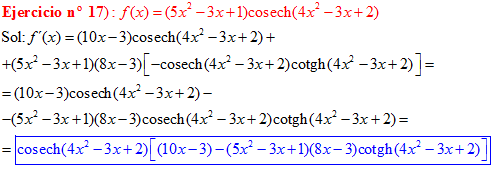
❊❊❊❊❊ FIN FÓRMULA 24 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO SENO HIPÉRBOLICO
|
FÓRMULA 25 compuesta
LA DERIVADA DEL ARGUMENTO SENO HIPERBÓLICO DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la función de x más la raíz cuadrada de la unidad más la función al cuadrado |
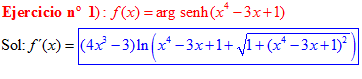
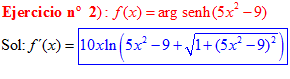
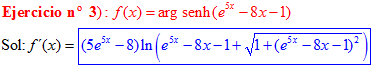
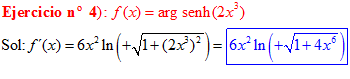
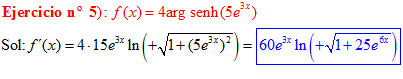
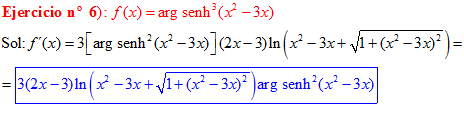


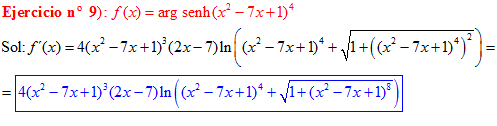
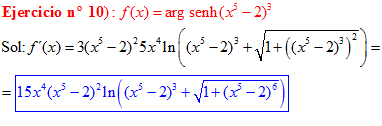
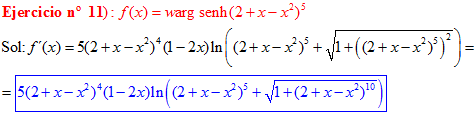
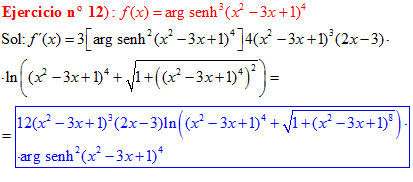
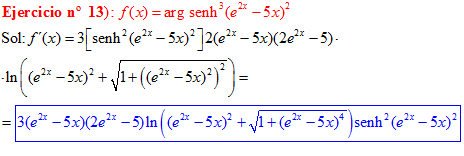
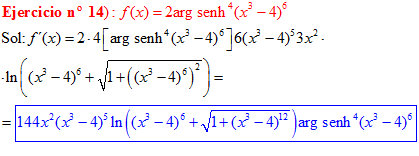
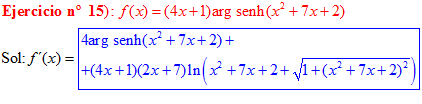
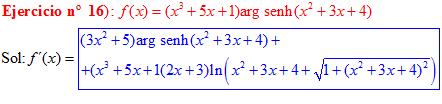
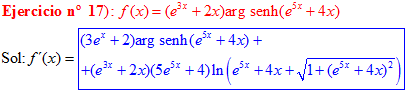
❊❊❊❊❊ FIN FÓRMULA 25 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COSENO HIPÉRBOLICO
|
FÓRMULA 26 compuesta
LA DERIVADA DEL ARGUMENTO COSENO HIPERBÓLICO DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la función de x más la raíz cuadrada de la función al cuadrado menos la unidad |
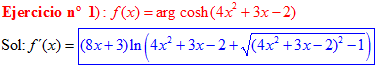
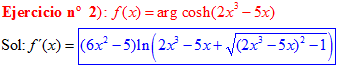

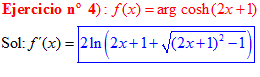
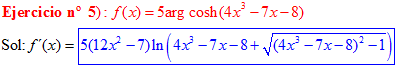
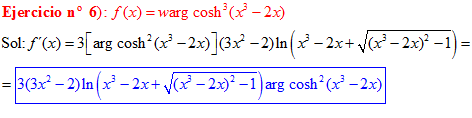
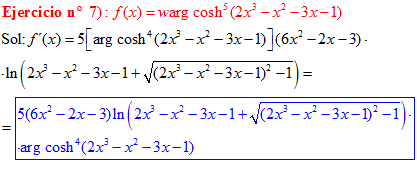
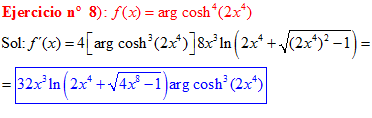
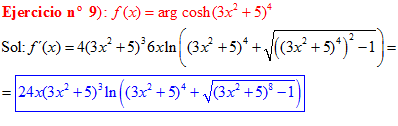
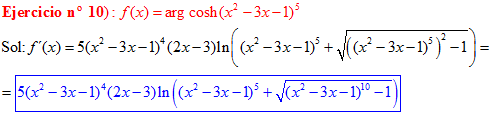
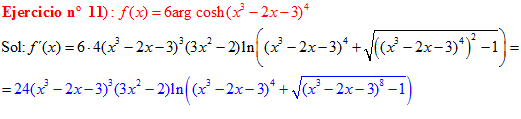
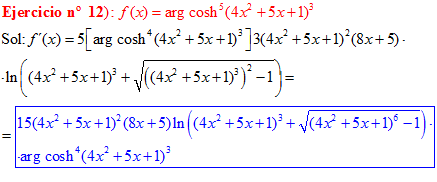
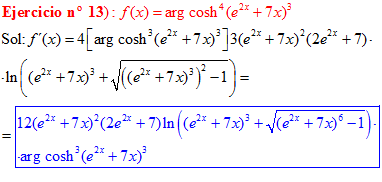
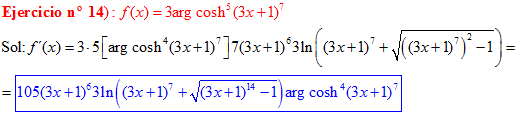
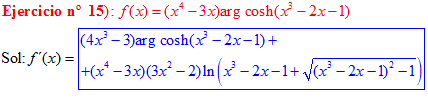
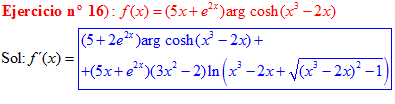
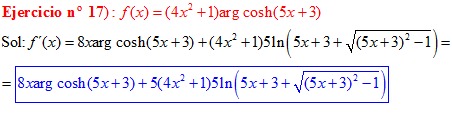
❊❊❊❊❊ FIN FÓRMULA 26 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO TANGENTE HIPÉRBOLICA
|
FÓRMULA 27 compuesta
LA DERIVADA DEL ARGUMENTO TANGENTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por un medio del logaritmo neperiano de uno más la función dividido entre uno menos la función de x |
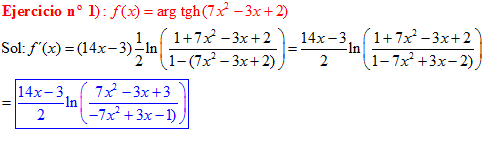
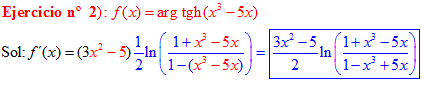
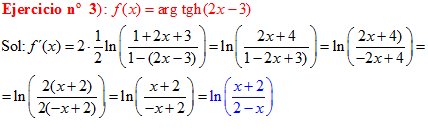
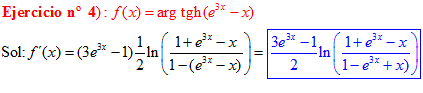
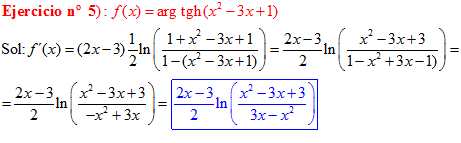
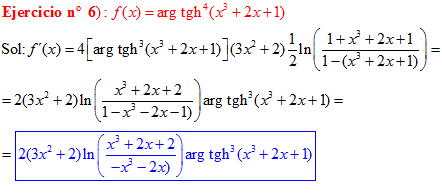
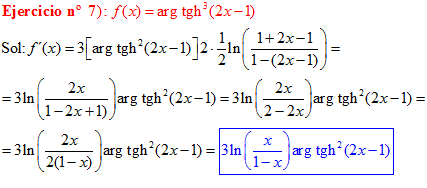
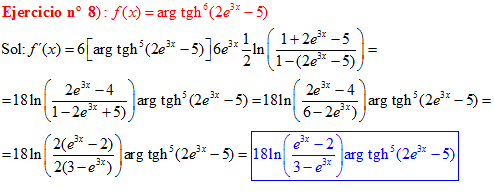
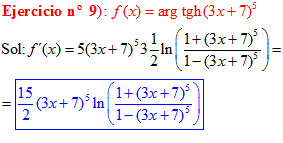
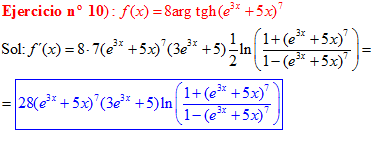
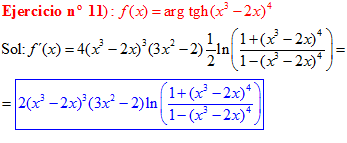
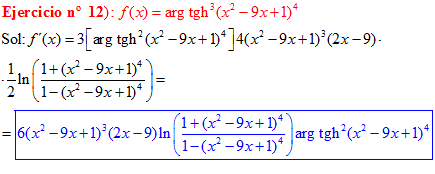
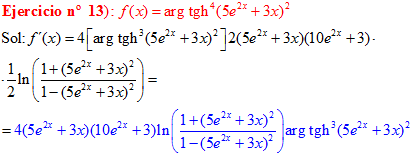
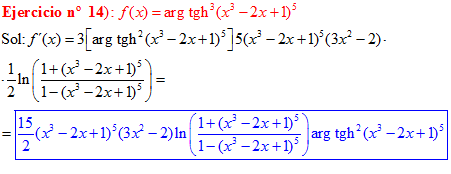
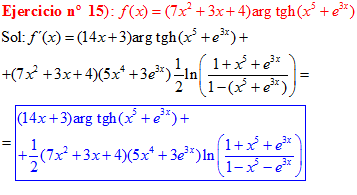
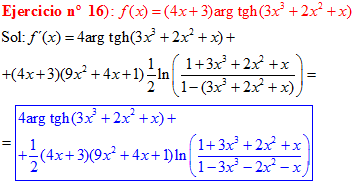
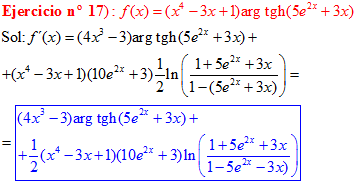
❊❊❊❊❊ FIN FÓRMULA 27 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COTANGENTE
HIPÉRBOLICA
|
FÓRMULA 28 compuesta
LA DERIVADA DEL ARGUMENTO COTANGENTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por un medio del logaritmo neperiano de la función más uno dividido entre la función menos uno |
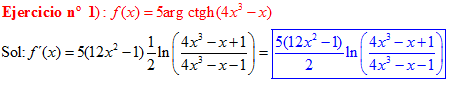
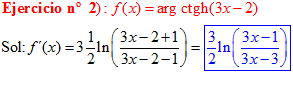
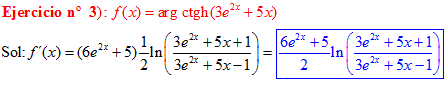
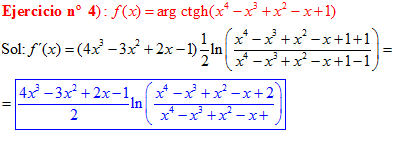
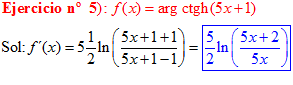
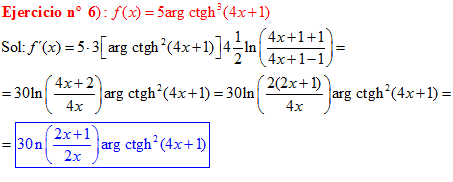
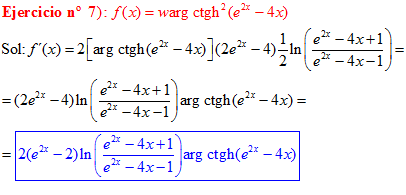
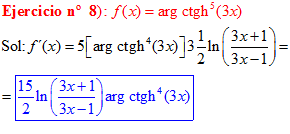
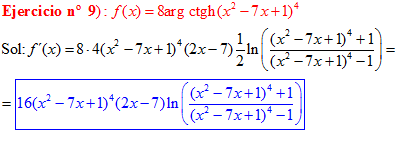
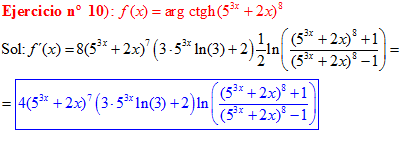
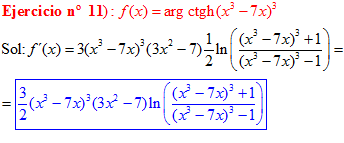
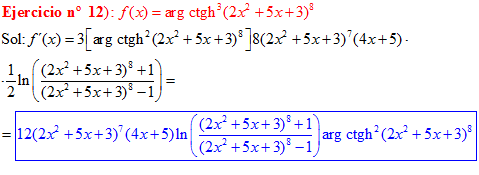
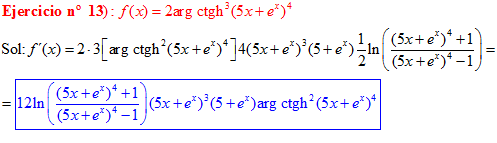
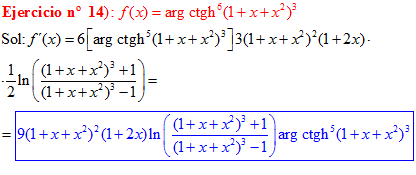
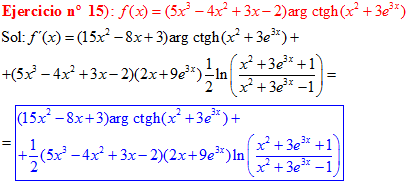
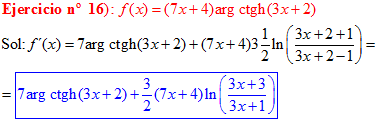
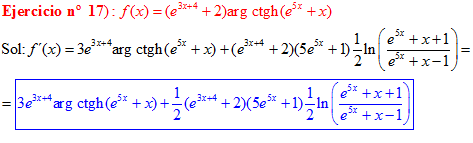
❊❊❊❊❊ FIN FÓRMULA 28 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO SECANTE HIPÉRBOLICA
|
FÓRMULA 29 compuesta
LA DERIVADA DEL ARGUMENTO SECANTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por el logaritmo neperiano del cociente de uno más la raíz cuadrada de uno menos la función al cuadrado dividido entre la función |
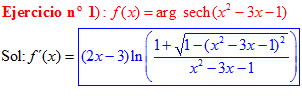
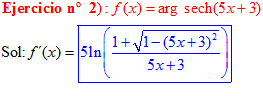
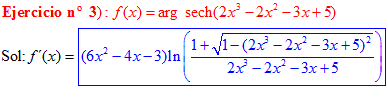
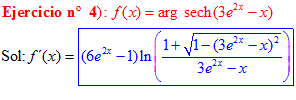
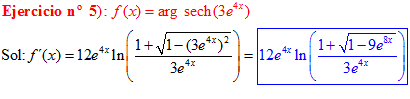



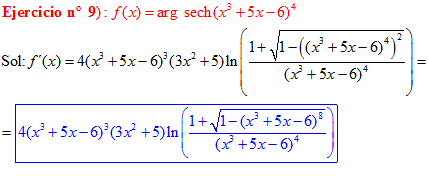
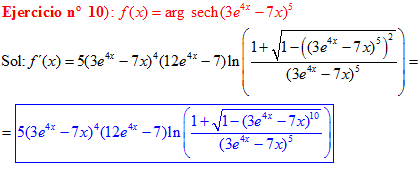
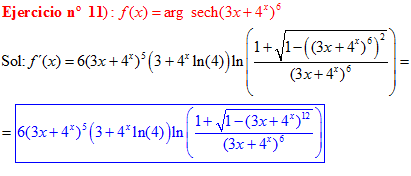
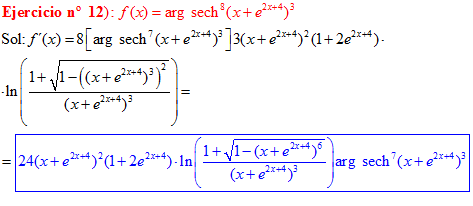
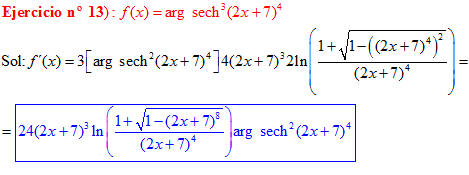
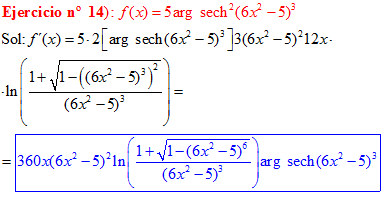
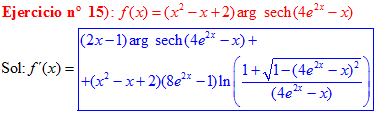
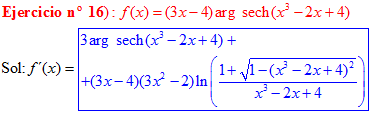
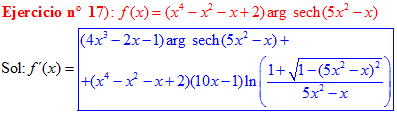
❊❊❊❊❊ FIN FÓRMULA 29 ❊❊❊❊❊
DERIVADA DE LA FUNCIÓN
ARGUMENTO COSECANTE
HIPÉRBOLICA
|
FÓRMULA 30 compuesta
LA DERIVADA DEL ARGUMENTO COSECANTE HIPERBÓLICA DE una función de x es igual a la derivada de la función por el logaritmo neperiano de la expresión uno partido por la función más la raíz cuadrada de uno más la función x partido por valor absoluto de la función |
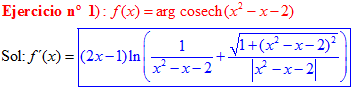
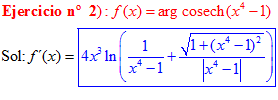

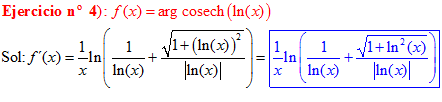
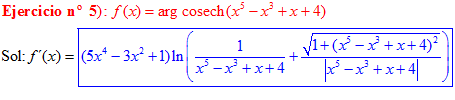

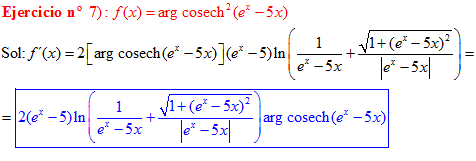
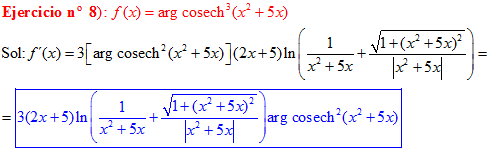
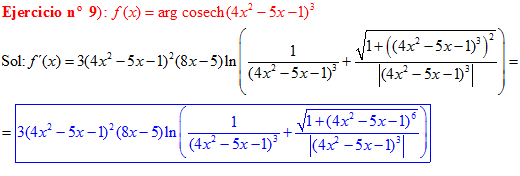

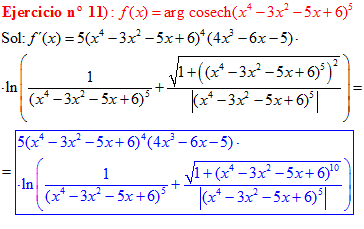
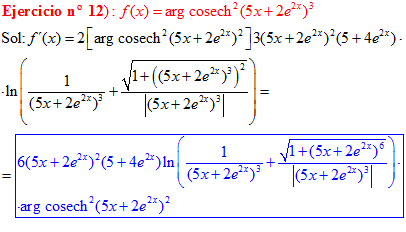

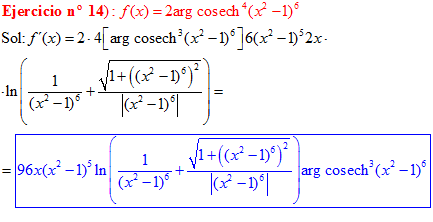
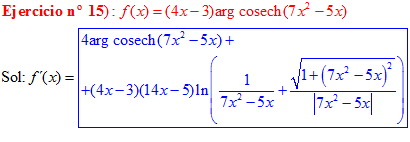
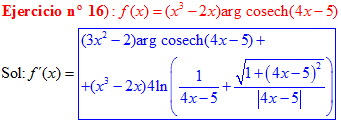
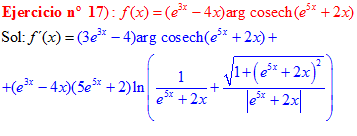
❊❊❊❊❊ FIN FÓRMULA 30 ❊❊❊❊❊

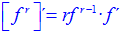
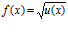
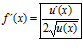
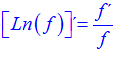
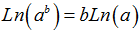
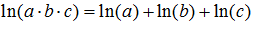
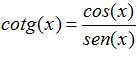
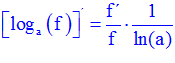
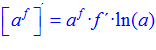
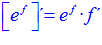
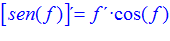
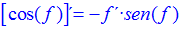
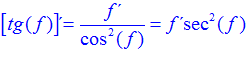
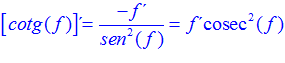
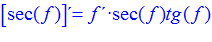
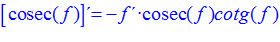
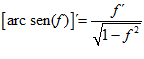
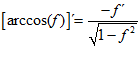
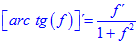
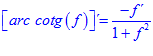
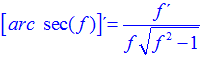
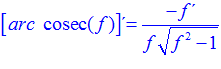
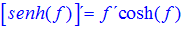
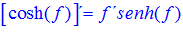
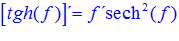
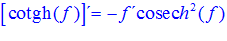
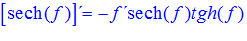
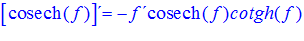
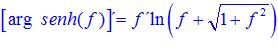
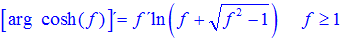
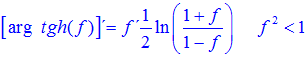
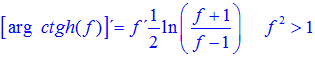
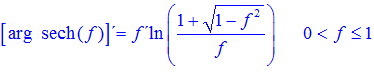
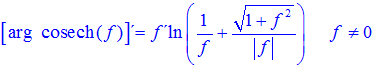
PERDÓN N2
creo que la n1esta mal, la de f(x)=(2x^3-4x^4+7)