¡Haz clic para puntuar!
(Votos: 1 Promedio: 5)
Las definimos por las siguientes fórmulas:
Derivada por la derecha: 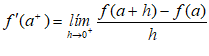
Derivada por la izquierda: 
Para que una función sea derivable en un punto tienen que existir las derivadas laterales y estas ser iguales.
Ejemplo 1:
Halla la derivada de la función  en el punto
en el punto 
Podemos seguir los siguientes pasos:
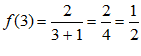 ;
;
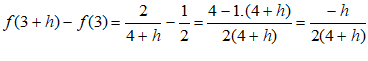

Ejemplo 2:
Dada la función  , halla la ecuación de la recta tangente en el punto de abscisa x = 2.
, halla la ecuación de la recta tangente en el punto de abscisa x = 2.
La pendiente de la recta tangente es el valor de la derivada:
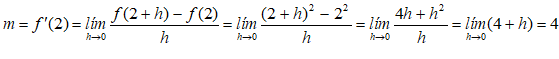
Las coordenadas del punto son:
Para x = 2, f(2) = 4 luego P(2, 4)
Aplicando la fórmula de la ecuación punto-pendiente:

Þ