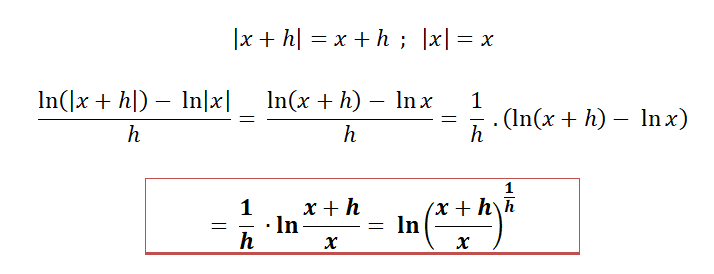La derivada de función logarítmica en base a es igual a la derivada de la función, dividida por la función, y a su vez por el logaritmo en base a de e.
Derivada de un logaritmo neperiano
El logaritmo neperiano, también conocido malamente como logaritmo natural, fueron descubiertos por primera vez por el gran John Neper. Estos logaritmos tienen base e y se representan como ln (x) o L(x).
Puesto que el logaritmo está definido sólo para valores positivos y distintos de cero, es necesario considerar el logaritmo del valor absoluto de x. Para hallar la derivada de esta función se han de considerar dos casos, x >0 y x <0:
Caso 1
Si x es positivo, aun tomando h negativo, x + h es positivo puesto que si se toman valores de h lo suficientemente pequeños, lo cual es permitido pues se va a calcular el límite cuando h tiende a cero, por tanto, se tiene lo siguiente en las condiciones ya tratada: