Visite nuestra página integrales.es
INICIACION A LA DERIVACIÓN
DERIVADAS UNA VARIABLE
1ª PARTE FORMAS SIMPLES
Versión 10-1-2014
|
TIPOS DE FORMULAS BÁSICAS DE DERIVACIÓN |
|||
|
1 |
 |
10 |
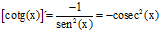 |
|
2 |
 |
11 |
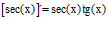 |
|
3 |
 |
12 |
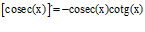 |
|
4 |
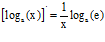 |
13 |
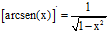 |
|
5 |
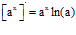 |
14 |
 |
|
6 |
 |
15 |
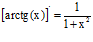 |
|
7 |
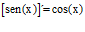 |
16 |
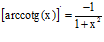 |
|
8 |
 |
17 |
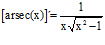 |
|
9 |
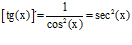 |
18 |
 |
|
REGLAS BÁSICAS DE DERIVACIÓN |
1ª) LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función: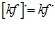 |
2ªa) LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones: |
2ªb) LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones: |
3ª) LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función: |
4ª) LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado: |
DERIVADA DE UNA COSTANTE
|
TIPO 1 forma simple
LA DERIVADA DE UNA CONSTANTE |

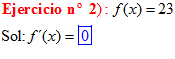
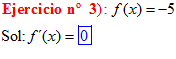

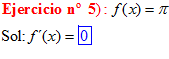

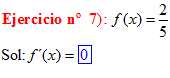
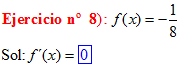
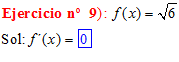
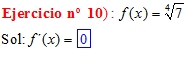
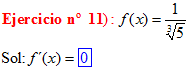


❊❊❊❊❊❊FIN TIPO 1❊❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN POTENCIAL
|
TIPO 2 forma simple
LA DERIVADA DE UNA FUNCIÓN POTENCIAL es igual al exponente por la variable elevado a una unidad menos |
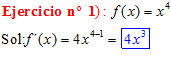


|
Regla nº 1
LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función |
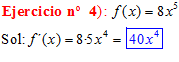
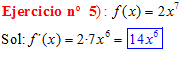

|
DERIVADAS Conviene que te acuerdes de:
LA DERIVADA DE X es igual a uno |
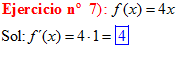

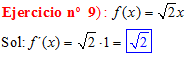
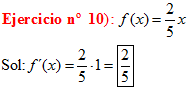
|
POTENCIAS Recuerda siempre que:
|

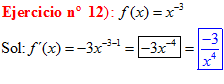


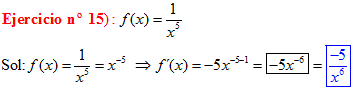

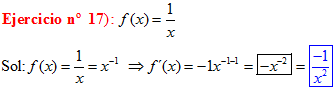
|
DERIVADAS Conviene que te acuerdes de:
LA DERIVADA DE UNO DIVIDIDO ENTRE x es igual a menos uno dividido entre x al cuadrado |


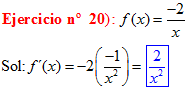
|
POTENCIAS Recuerda siempre que:
|


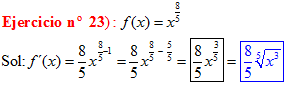



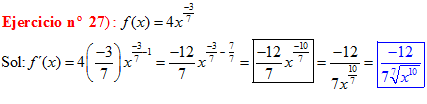

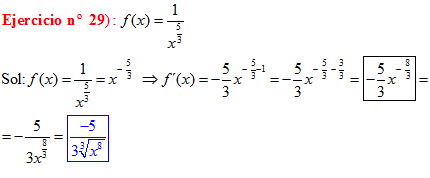
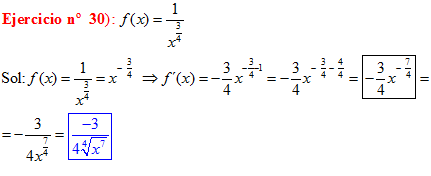

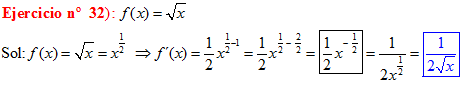
|
DERIVADAS Conviene que te aprendas:
LA DERIVADA DE LA RAIZ CUADRADA DE X es igual a la unidad dividida entre dos veces la raíz cuadrada de X |


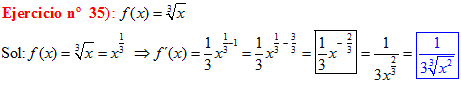
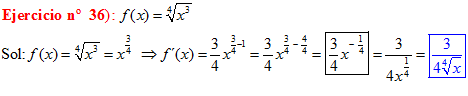
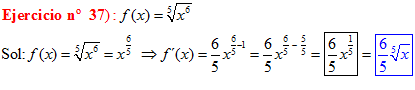
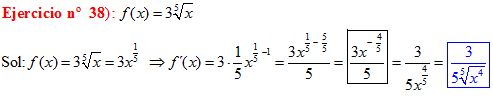
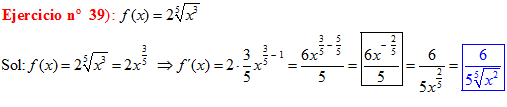
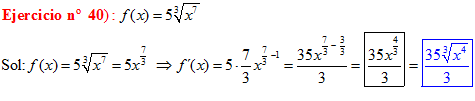

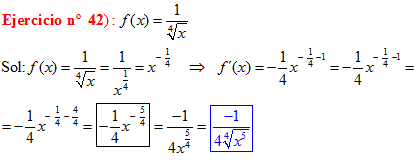



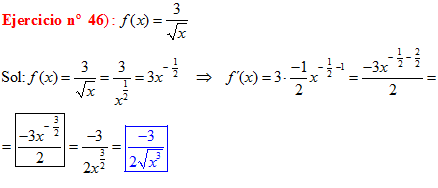


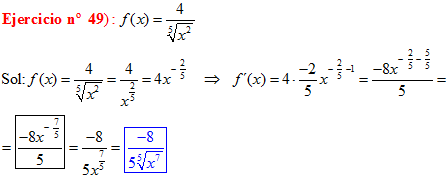
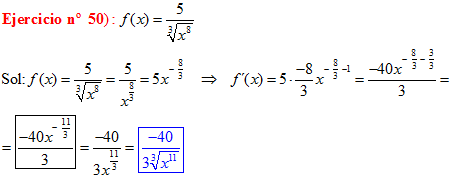
|
Regla nº 2
LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones |
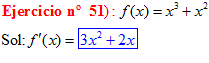
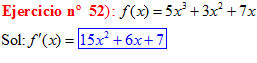
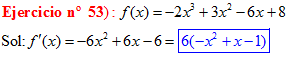

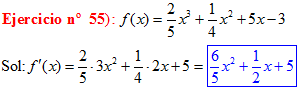
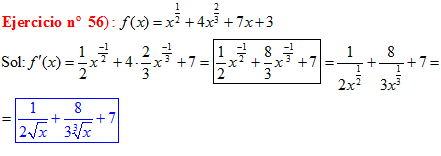
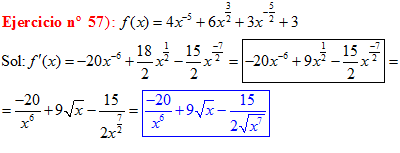
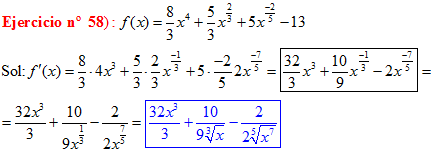
|
Regla nº 3
LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función |
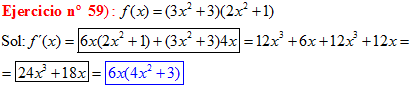
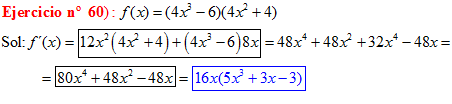
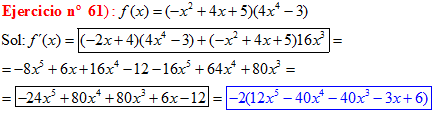

|
Regla nº 4
LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado |
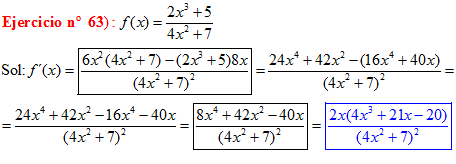

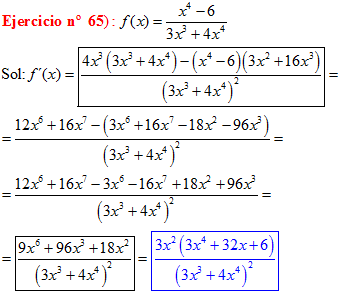


❊❊❊❊❊❊FIN TIPO 2❊❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN LOGARÍTMICA
|
TIPO 3 forma simple
LA DERIVADA DEL LOGARITMO NEPERIANO DE x es igual a la unidad dividida entre x |
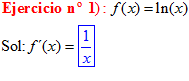




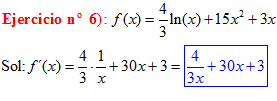
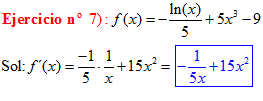
❊❊❊❊❊❊FIN TIPO 3❊❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN LOGARÍTMICA CON BASE DISTINTA DEL NÚMERO e
|
TIPO 4 forma simple
LA DERIVADA DEL LOGARITMO EN BASE a DE x es igual a la unidad dividida entre x por el logaritmo en base a del número e |
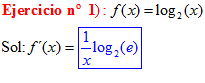
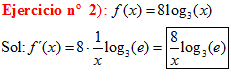


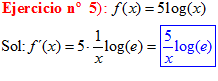
❊❊❊❊❊❊FIN TIPO 4❊❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN EXPONENCIAL CON BASE DISTINTA DEL NÚMERO e
|
TIPO 5 forma simple
LA DERIVADA DE UNA CONSTANTE «a» ELEVADO A LA VARIABLE x es igual a la misma constante «a» elevada a x por el logaritmo neperiano de dicha constante |

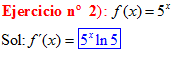
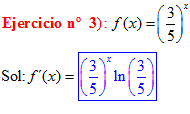
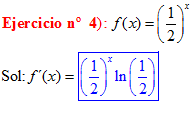




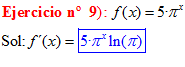
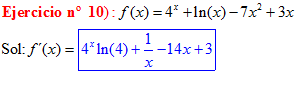
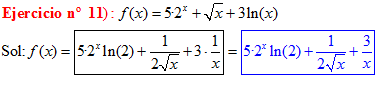
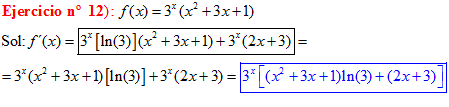
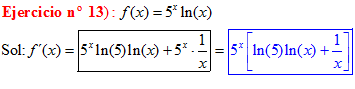
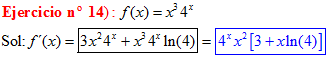



❊❊❊❊❊❊FIN TIPO 5❊❊❊❊❊❊
DERIVADA DE UNA FUNCIÓN EXPONENCIAL CON BASE EL NÚMERO e
|
TIPO 6 forma simple
LA DERIVADA DEL NÚMERO e ELEVADO A LA VARIABLE x es igual al número e elevado a dicha variable |
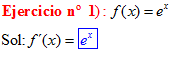

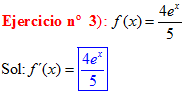
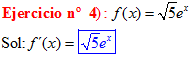

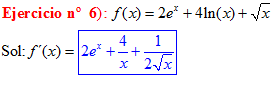


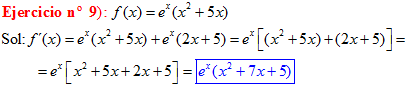

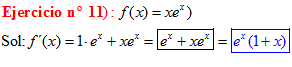


|
POTENCIAS Recuerda siempre que:
POTENCIA DE UNA POTENCIA es igual a la misma base elevada al producto de los exponentes |
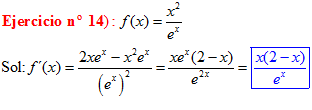

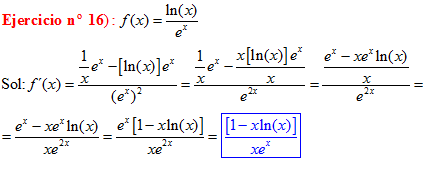
❊❊❊❊❊❊FIN TIPO 6❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA SENO
|
TIPO 7 forma simple
LA DERIVADA DEL SENO DE x igual a coseno de x |




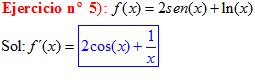
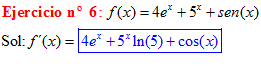
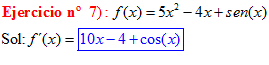
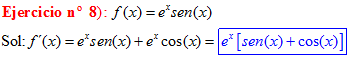



|
POTENCIAS Recuerda siempre que:
|


|
FRACCIONES Recuerda siempre que:
|

|
POTENCIAS Recuerda siempre que:
|

❊❊❊❊❊❊FIN TIPO 7❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COSENO
|
TIPO 8 forma simple
LA DERIVADA DEL COSENO DE x igual a menos seno de x |
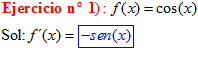
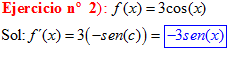
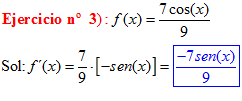
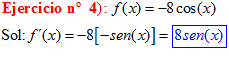

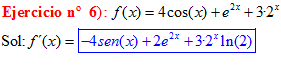
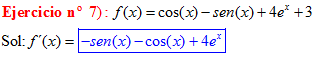


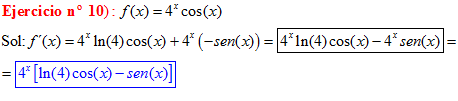

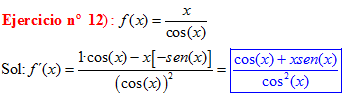

|
TRIGONOMETRÍA Recuerda siempre que:
LA FÓRMULA FUNDAMENTAL DE LA TRIGONOMETRÍA ES: el seno cuadrado de un ángulo mas el coseno cuadrado del mismo ángulo es igual a la unidad |

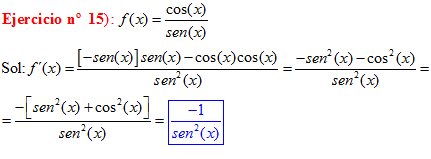
❊❊❊❊❊❊FIN TIPO 8❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA TANGENTE
|
TIPO 9 forma simple
LA DERIVADA DE LA TANGENTE DE x es igual a la unidad dividida por el coseno cuadrado de x |
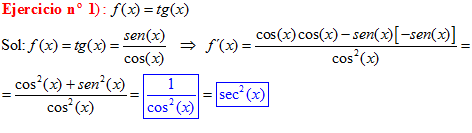
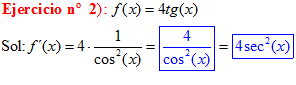

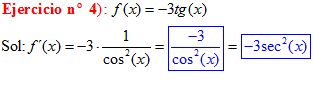 Sol:
Sol:



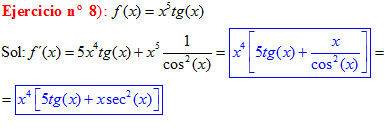
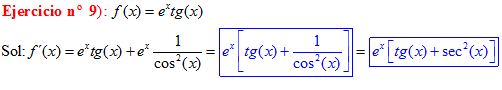

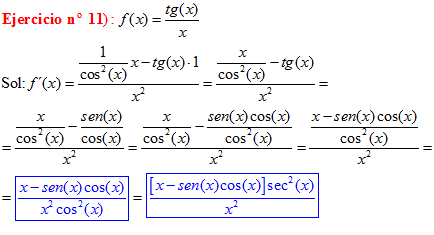
|
TRIGONOMETRÍA Recuerda siempre que:
LA TANGENTE DE UN ÁNGULO es igual al seno de dicho ángulo dividido entre el coseno del mismo |

❊❊❊❊❊❊FIN TIPO 9❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COTANGENTE
|
TIPO 10 forma simple
LA DERIVADA DE LA COTANGENTE DE x es igual a menos la unidad dividida por el seno cuadrado de x |
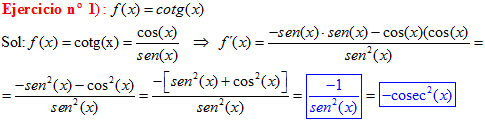
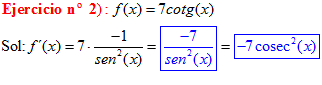

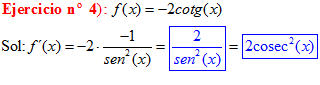 Sol:
Sol:


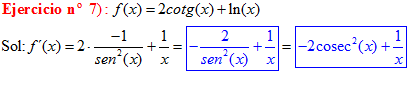
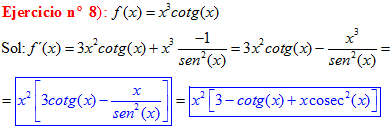
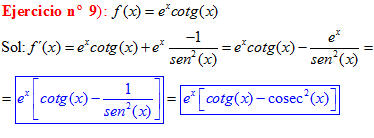
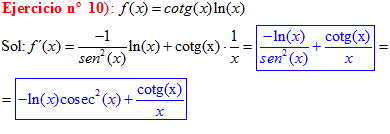
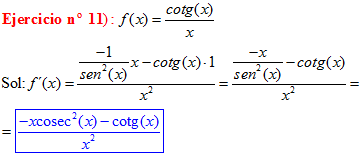
|
TRIGONOMETRÍA Recuerda siempre que:
LA COTANGENTE DE UN ÁNGULO es igual al coseno de dicho ángulo dividido entre el seno del mismo |
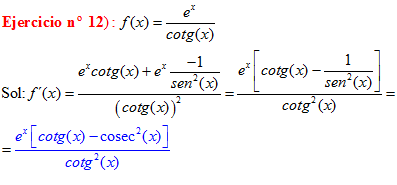
❊❊❊❊❊❊FIN TIPO 10❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA SECANTE
|
TIPO 11 forma simple
LA DERIVADA DEL SECANTE DE x es igual a secante de x por tangente de x |


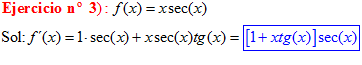
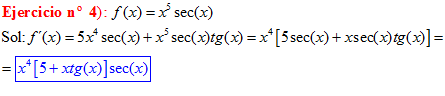



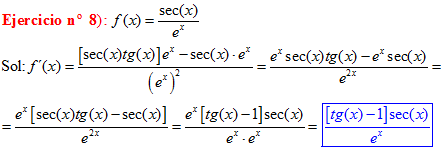
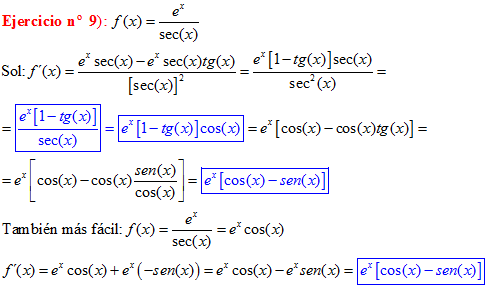
❊❊❊❊❊❊FIN TIPO 11❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA COSECANTE
|
TIPO 12 forma simple
LA DERIVADA DEL COSECANTE DE x es igual a menos cosecante de x por tangente de x |
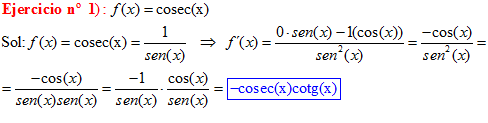


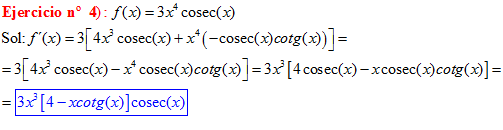

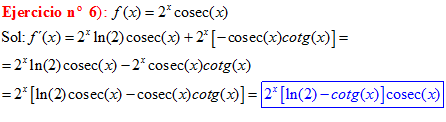
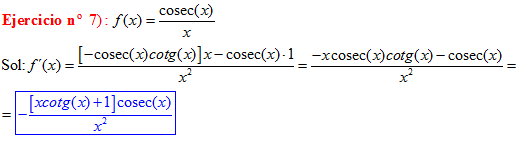

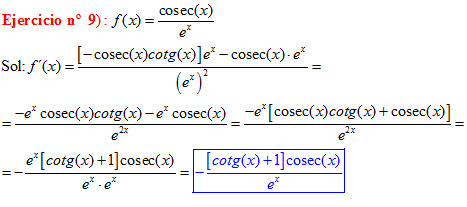

❊❊❊❊❊❊FIN TIPO 12❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO SENO
|
TIPO 13 forma simple
LA DERIVADA DEL ARCO SENO DE x es igual a la unidad dividida entre la raíz cuadrada de uno menos la variable x al cuadrado |


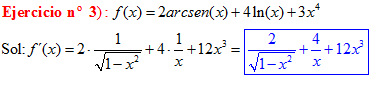
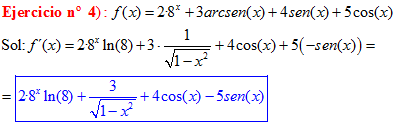
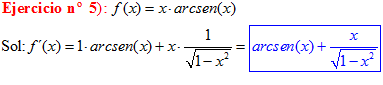

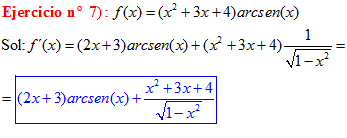

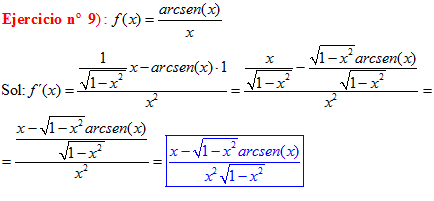
❊❊❊❊❊❊FIN TIPO 13❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COSENO
|
TIPO 14 forma simple
LA DERIVADA DEL ARCO SENO DE x es igual a la unidad dividida entre la raíz cuadrada de uno menos la variable x al cuadrado |
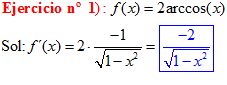
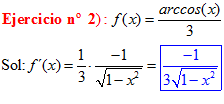
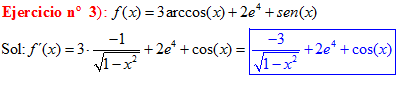
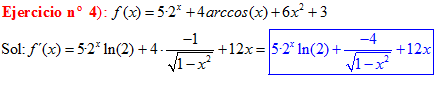
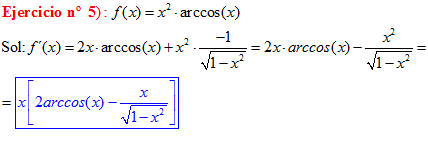
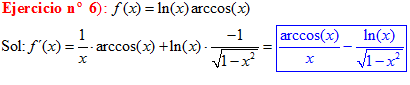
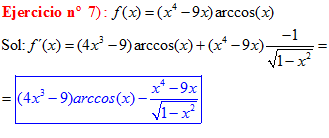
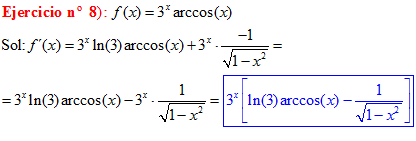
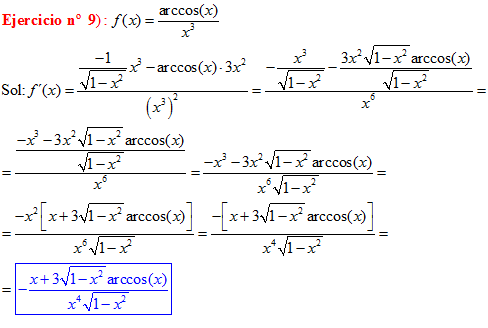
❊❊❊❊❊❊FIN TIPO 14❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO TANGENTE
|
TIPO 15 forma simple
LA DERIVADA DEL ARCO TANGENTE DE x es igual a la unidad dividida entre uno mas la variable x al cuadrado |
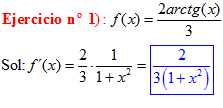
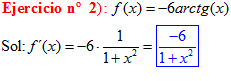


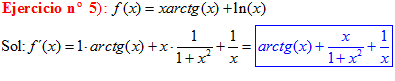


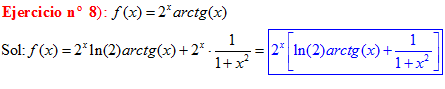


❊❊❊❊❊❊FIN TIPO 15❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COTANGENTE
|
TIPO 16 forma simple
LA DERIVADA DEL ARCO COTANGENTE DE x es igual a menos la unidad dividida entre uno mas la variable x al cuadrado |

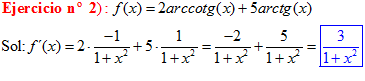

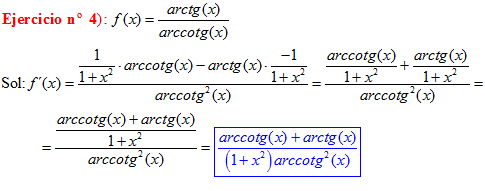

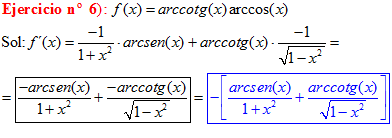




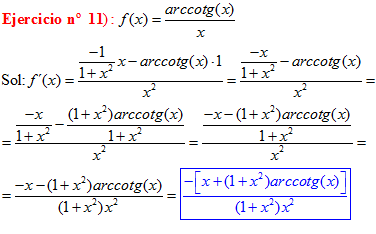


❊❊❊❊❊❊FIN TIPO 16❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO SECANTE
|
TIPO 17 forma simple
LA DERIVADA DEL ARCO SECANTE DE x es igual a la unidad dividida entre x por la raíz cuadrada de x al cuadrado menos uno |




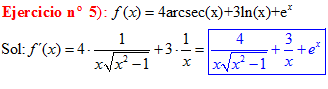
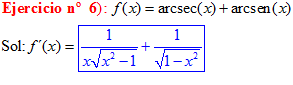

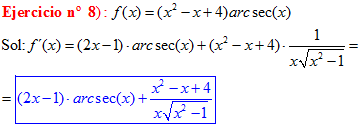
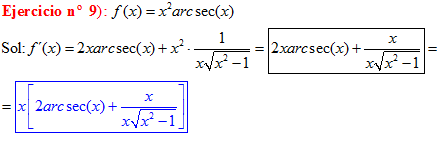
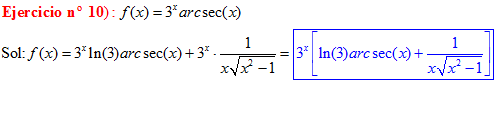
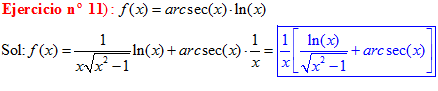


❊❊❊❊❊❊FIN TIPO 17❊❊❊❊❊❊
DERIVADA DE LA FUNCIÓN TRIGONOMÉTRICA ARCO COSECANTE
|
TIPO 18 forma simple
LA DERIVADA DEL ARCO COSECANTE DE x es igual a menos la unidad dividida entre x por la raíz cuadrada de x al cuadrado menos uno |

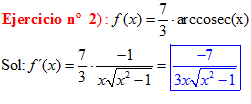
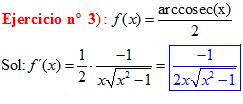
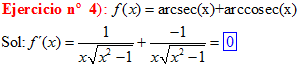
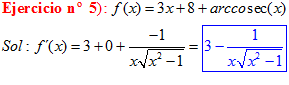
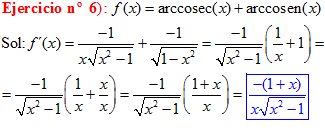
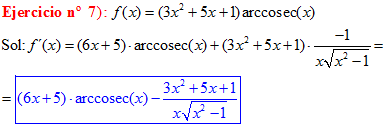

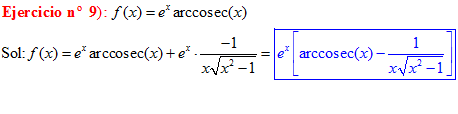



❊❊❊❊❊❊FIN TIPO 18❊❊❊❊❊❊





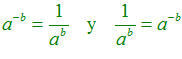
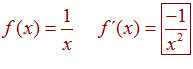

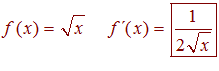
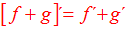
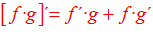

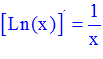
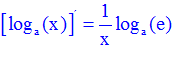
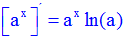
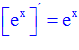


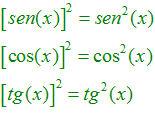
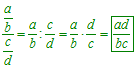




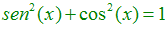
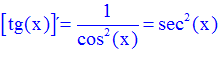
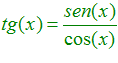
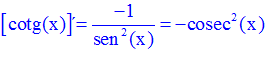
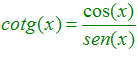
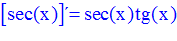
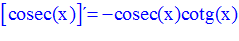
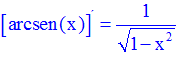

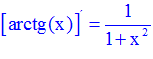

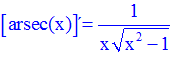
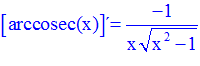
me parecio un poco largo el tema pero esta muy bien explicado todo pero sin embargo agradecesia al profesor que me explique en clse
El tema esta biem explicado Gracias
profesor el tema esta muy biem explicado y eso nos ayuda a entender muy biem el tema
bastante largo pero bueno con tal de aprender es tan bien gracias…
PROFE PORQUE TAN LARGO.. PARA ENSEÑARNOS NO SE NECESITA DARNOS TODO ESO DEBERIA SER ALGO CORTO EXAPTO Y PRECISO NO ALGO Q NO ENTENDAMOS PERO MUCHAS GRACIAS POR TODO…
profesor este tema de derivadas esta muy largo , pero con la informacion y los videos lo podre entender gracias por hacer este tema mas facil con videos y ejemlos es una forma muy practica de aprender
profesor este tema de derivadas esta muy largo , pero con la informacion y los videos lo podre entender gracias por hacer este tema mas facil con videos y ejemlos
el tema es un poco extenso, pero con un refuerzo en clase estaremos listos… gracias
gracias a este medio, podemos nutrirnos de una información completa, la cual no es posible no la faciliten en horas de clase ya que el tiempo es poco, pero le agradezco profesor, porque usted esta demostrando la importancia de un grado 11
profesor esta un poco largo ….
pero bueno ya lo copie todo
gracias por la informacion es muy explicita.