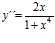Ejercicios resueltos de derivadas, límites y continuidad.
1. (Sydsaeter, prob. 1 de pág. 89 y prob. 9a de pág. 90). Dada la función f(x) = 4x2, deducir razonadamente f ‘(5).
2. Halla, utilizando la definición, la derivada de la función 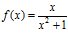 en el punto x = 2.
en el punto x = 2.
Comprueba aplicando las reglas de derivación que tu resultado es correcto. (Sol. –3/25)
3. Aplicando la definición demuestra que la función 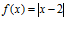 no es derivable en x = 2. Da también un razonamiento gráfico.
no es derivable en x = 2. Da también un razonamiento gráfico.
4. Dada la función 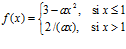
a) ¿Para qué valores del parámetro a es continua? b) ¿Para qué valores de a es derivable?
(Sol. a) 1 o 2; b) 1)
5. Dada la función 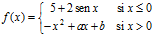
- ¿Para qué valores de los parámetros a y b es continua la función f (x)?
-
Determina a y b para que f(x) sea derivable en x = 0.
(Sol. b = 5; a = 2)
6. Calcula, simplificando el resultado, la derivada de la función:
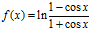 . Sol.
. Sol.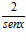
7. Deriva y simplifica: a)
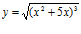 b)
b) 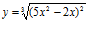
Sol. a)
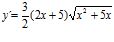 ;b)
;b) 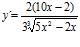
8. Para las funciones del problema anterior, indica los puntos en los que la derivada vale 0.
(Sol.
a) Nunca; b) 1/59. Deriva: a)
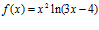 b)
b) 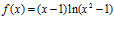 c)
c) 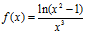
Sol. a)
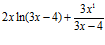 ; b)
; b) 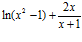 ; c)
; c) 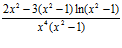
10. Deriva: a)
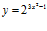 b)
b) 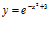 c)
c) 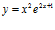 d)
d) 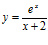
Sol. a)
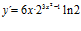 ; b)
; b) 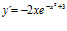 ; c)
; c) 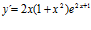 ; d)
; d) 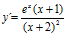
11. Si
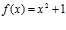 y
y 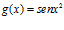 halla la derivada de las funciones
halla la derivada de las funciones  y
y 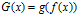 , aplicando la regla de la cadena. (Sol.
, aplicando la regla de la cadena. (Sol. 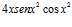 ;
; 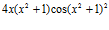 )
)12. (Sydsaeter, prob. 15 de pág. 122). Si R = Sa, S = 1 + bKg y K = Atp + B, hallar dR/dt.
13. Halla la ecuación de la recta tangente a
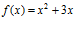 en el punto x = –1. Representa gráficamente la curva y la tangente. (Sol.
en el punto x = –1. Representa gráficamente la curva y la tangente. (Sol. 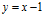 )
)
14. Halla la ecuación de la recta tangente a
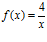 en el punto de abscisa x = 4. (S.
en el punto de abscisa x = 4. (S.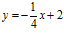 )
)
15. Halla los puntos de la curva
 en los que su tangente tiene pendiente 1. Halla la ecuación de esas tangentes. (Sol. y = x + 2 e y = x –2.)
en los que su tangente tiene pendiente 1. Halla la ecuación de esas tangentes. (Sol. y = x + 2 e y = x –2.)
16. Comprueba que, en el punto x = 1, la función
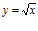 puede aproximarse por la recta
puede aproximarse por la recta 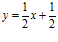 . Utiliza ese resultado para hallar la raíz cuadrada de 1,1. (Sol.
. Utiliza ese resultado para hallar la raíz cuadrada de 1,1. (Sol. 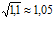 )
)
17. (Sydsaeter, prob. 5a y 5e de pág. 131).Probar que (1 + x)m
» 1 + mx, para x próximo a 0, y usar lo anterior para hallar aproximaciones de los números siguientes:a) 1,11/3 = (1+ 1/10)1/3 b)
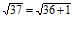
18. Calcula la diferencial de la función tag x en el punto
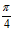 para Dx = dx = 0,01. (Sol. 0,02.)
para Dx = dx = 0,01. (Sol. 0,02.)19. (Sydsaeter, prob. 7 de pág. 131) El radio de una esfera aumenta de 2 a 2,03. Estimar el aumento de volumen usando una aproximación lineal. Comparar con el aumento real del volumen.
20. (J/94). La derivada de orden n de
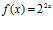 es:
es:(a)
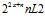 (b)
(b) 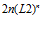 (c)
(c) 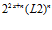
21. Halla la derivada n-ésima de
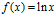 . (Sol.
. (Sol.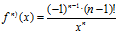
22. (S/98). La función
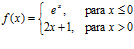 , en el punto x = 0 es:
, en el punto x = 0 es: -
Derivable pero no continua. b) Continua pero no derivable. c) Continua y derivable.
23. Dada la función:
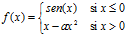
¿Existen valores de a para los cuales f sea derivable en toda la recta real? (Sol. para todo a.)
24. (F–04). La función
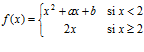 es derivable en x = 2 si:
es derivable en x = 2 si:
- b = –2a b) Sólo si a = –2 y b = 4 c) Ninguna de las anteriores.
25- (S–99)
La derivada de la función 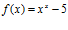 se anula en al menos un punto del intervalo
se anula en al menos un punto del intervalo
a) (1, 5) b) [5, 10] c) Ninguna de las anteriores.
26. (F–02) Dada 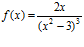 , los valores de f ´(1) y f ´´(1) son, respectivamente:
, los valores de f ´(1) y f ´´(1) son, respectivamente:
a) 1 y 14 b) –1 y 4 c) –1 y –21/4
27. (F–02) La ecuación de la recta tangente a la curva 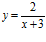 en el punto de abscisa x = 1 es:
en el punto de abscisa x = 1 es:
a) 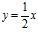 b)
b) 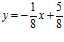 c) y = 2x
c) y = 2x
28. Deriva: a) 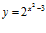 b)
b)  c)
c) 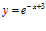 d)
d) 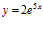 e)
e) 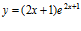
Sol.
a)  ; b)
; b) 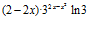 ; c)
; c) 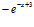 ; d)
; d) 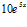 e)
e) 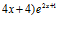
29. Deriva: a) 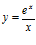 b)
b) 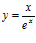 c)
c) 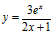 d)
d) 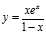 e)
e) 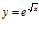 f)
f) 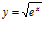
Sol.
a) 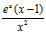 ; b)
; b) 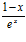 ; c)
; c) 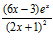 ; d)
; d) 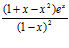 ; e)
; e) 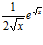 ; f)
; f) 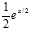
Otros ejercicios (Sacados de 1º Bachillerato, McGraw–Hill; 2007)
30. Halla la derivada de las siguientes funciones:
a) 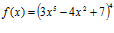 b)
b) 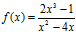 c)
c) 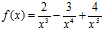
d) 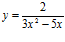 e)
e) 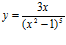
Solución:
a) 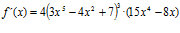 ; b)
; b) 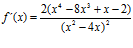 ;
;
c) 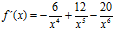 ; d)
; d) 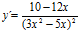 ; e)
; e) 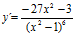
31. Deriva y simplifica (piensa si puedes utilizar las propiedades de los logaritmos):
a) 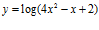 b)
b) 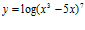 c)
c) 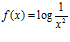 d)
d) 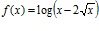
Solución:
a) 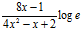 ; b)
; b) 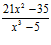 ; c)
; c) 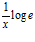 ; d)
; d) 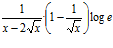
32. Deriva:
a) 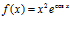 ; b)
; b) 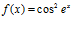 ; c)
; c) 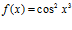 ; d)
; d) 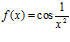 ; e)
; e) 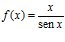
Solución:
a) 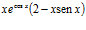 ; b)
; b) 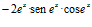 ; c)
; c) 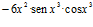 ; d)
; d)  ;
;
e) 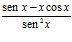 ;
;
33. Deriva y simplifica cuando sea posible:
a) 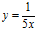 b)
b)  c)
c) 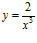 d)
d) 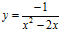 e)
e) 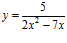
[sol] a) 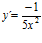 ; b)
; b) 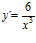 ; c)
; c) 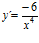 ; d)
; d) 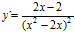 ; e)
; e) 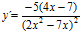
34. Deriva y simplifica:
a) 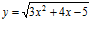 b)
b) 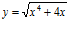 c)
c) 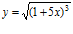 d)
d) 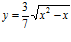
[sol] a) 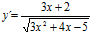 ; b)
; b) 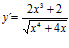 ; c)
; c) 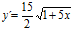 ; d)
; d) 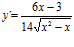
35. Deriva y simplifica:
a) 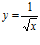 b)
b) c)
c) 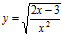
[sol] a) 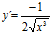 ; b)
; b) 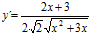 ; c)
; c) 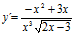 ; e)
; e)
36. Deriva:
a) 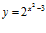 b)
b) 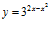 c)
c) 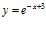 d)
d) 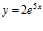 e)
e) 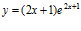
[sol] a) 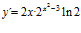 ; b)
; b) 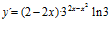 ; c)
; c) 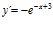 ; d)
; d) 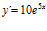
e) 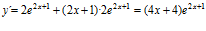
37. Deriva:
a) 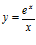 b)
b) 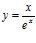 c)
c) 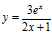 d)
d) 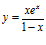 e)
e) 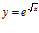 f)
f) 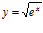
[sol] a) 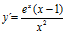 ; b)
; b) 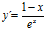 ; c)
; c) 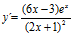 ; d)
; d) 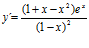
e) 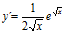 ; f)
; f) 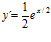
38. Deriva y simplifica (piensa si puedes utilizar las propiedades de los logaritmos):
a) 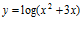 b)
b) 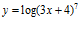 c)
c) 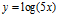 d)
d) 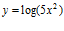
e) 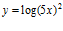 f)
f) 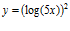 g)
g)  h)
h) 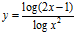
[sol] a) 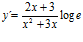 ; b)
; b) 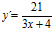 ; c)
; c) 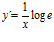 ; d)
; d) 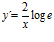 ; e)
; e) 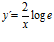 ;
;
f) 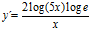 ; g)
; g) 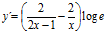 ; h)
; h) 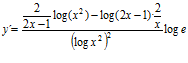
39. Deriva y simplifica (piensa si puedes utilizar las propiedades de los logaritmos):
a) 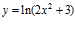 b)
b) 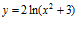 c)
c) 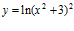
d) 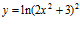 e)
e) 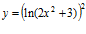
[sol] a) 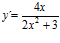 ; b)
; b) 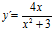 ; c) Idem; d)
; c) Idem; d) 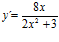 ; e) y´=
; e) y´=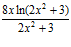
40. a)  b)
b) 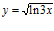 c)
c) 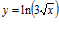 d)
d) 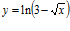
[sol] a) 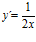 ; b)
; b) 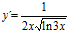 ; c)
; c) 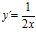 ; d)
; d) 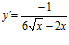
41. a) 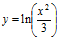 b)
b) 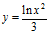 c)
c) 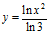
[sol] a) 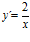 ; b)
; b) 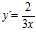 ; c)
; c) 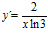
42. Deriva:
a)  b)
b) 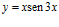 c)
c) 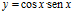 d)
d) 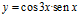
[sol] a) 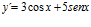 ; b)
; b) 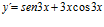 ; c)
; c) 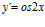 ;
;
d) 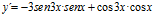
43. Deriva:
a) 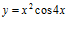 b)
b) 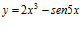 c)
c) 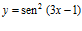 d)
d) 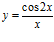
[sol] a) 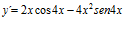 ; b)
; b)  ;
;
c) 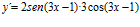 ; d)
; d) 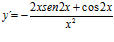
44. Deriva:
a) 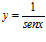 b)
b) 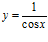 c)
c) 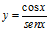
[sol] a) 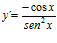 ; b)
; b) 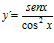 ; c)
; c) 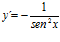
45. Deriva:
a) 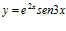 b)
b) 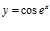 c)
c) 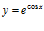
[sol] a) 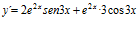 ; b)
; b) 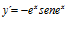 ; c)
; c) 
46. Deriva:
a) 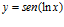 b)
b) 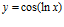 c)
c) 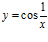 d)
d) 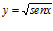
[sol] a) 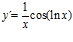 ; b)
; b) 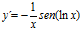 ; c)
; c) 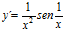 ; d)
; d) 
47. Deriva:
a)  b)
b) 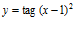 c)
c) 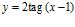
d) 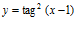 e)
e) 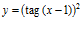
[sol] a) 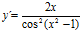 ; b)
; b) 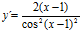 ; c)
; c) 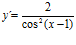
d) 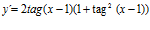 ; e) Idem.
; e) Idem.
48. Deriva:
a) 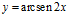 b)
b) 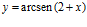 c)
c) 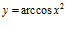
d) 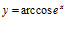 e)
e) 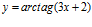 f)
f) 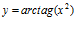
[sol] a) 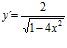 ; b)
; b) 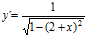 ; c)
; c) 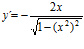
d) 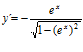 ; e)
; e)  ; f)
; f)