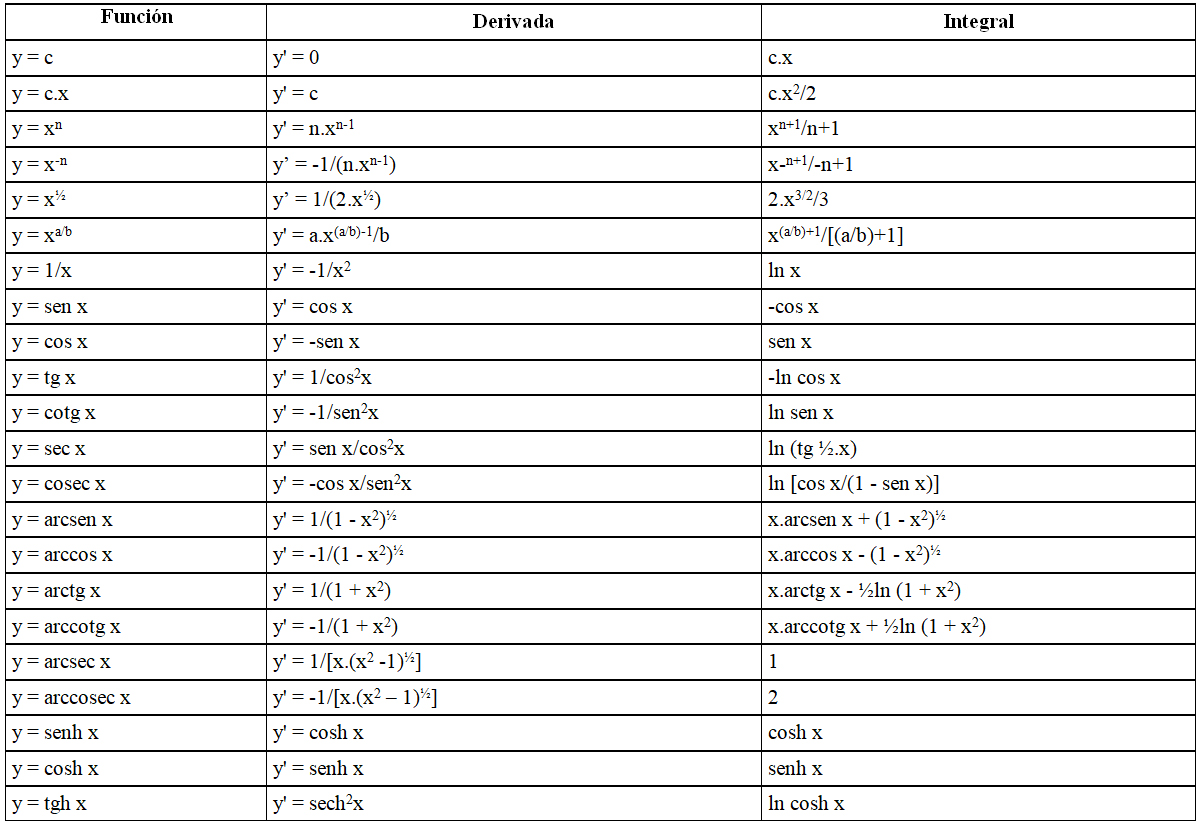
Te mostramos las tablas de derivadas e integrales compuestas por una función y su correspondiente derivada, y también se incluye la integral de la función.
Casi cualquier estudiante de matemáticas avanzadas, ingenieros y físicos ha tenido que trabajar con tablas de derivadas y tablas de integrales en algún momento de la carrera, o también posteriormente.
Nuestra página web está formada por los mejores profesores y han redactado al completo todo el tema de las derivadas, para que todo aquel que busque información la comprenda.
ÍNDICE
¿Qué es importante para comprender las derivadas?
Seguramente te interese también conocer como funcionan las integrales para ello hemos hecho una tabla entera con todos los tipos de integrales que existen:
Explicaciones y resoluciones importantes
Hay algunas explicaciones y soluciones de derivadas que son muy importantes de conocer. Por ello, te dejamos un listado con todo lo que deberías de echarle un vistazo:
- Explicación de la derivada de e^x. Para entenderla fácilmente la hemos demostrado de principio a fin.


A ver expertos en matemáticas, lo que ha dicho Joseba es cierto, porque la derivada de x es x`=1 asi que si
f (x) = x^n
f ‘(x) = x’ n x^n-1
Y como x’=1 pues queda f ‘(x) = n x^n-1.
Bueno ahí os quedaís.
encima os quejais? esta muy bien la tabla. Gracias por la aportacion.
Y a estos que se quejan les digo…¿por que no habeis hecho la tabla vosotros? ^^
luis tu te refieres a la parcial de (xy)^1/2 con respecto a x
como es con respecto a x trataremos a y como una cte, luego la derivada que tu pides simplemente se convierte en la derivada de la raíz cuadrada de una variable por una cte (sea c = y ) (donde c es cte)
lo que es igual a (cx)^1/2 y su derivada es igual a x/ (cx)^1/2
y eso es todo Saludos!!
Me parece que esta muy bien tu informacion acerca de las derivadas e integrales. saludos
cual es la derivada de (x*y)^1/2 con respecto a x
por ejemplo Y=u^2 (donde u=x+1)
Y’=[(x+1)^2]’
Y’=2(x+1).x = 2u.u’
Creo que hay un error, u`= 1 (porque x`= 1 y 1′ = 0)
Por lo tanto. Si Y=u^2 (donde u=x+1)
Y’ = 2*(x+1)*1 = 2*(x+1) = 2*u*u’
( Donde «*» es «multiplicar» NO convolución. )
Un saludo!!
:???? WTF!!!
Si que está bien esa derivada!!!!!! No lies al personal!! Uno poco mas y me caigo de la silla con tu comentario :S :S :S
Tu, mister pamplinas, eso solo es correcto si y=[f(x)]^n, asi que callate la boca melindres.
No joseba, estas interpretando mal la tabla.
ejemplo: Y=x^2
ahora si derivo «x al cuadrado»: Y’=2x
como veras x es una variable, y n=2.
Lo que vos decis es cuando tratas a x como una función en si misma, y ahi utilizas la regla de la cadena (derivando primero lo de «afuera» y multiplicando por la derivada de lo de adentro).
en la tabla, la X que vos usas, ellos la expresan como u.
por ejemplo Y=u^2 (donde u=x+1)
Y’=[(x+1)^2]’
Y’=2(x+1).x = 2u.u’
Lo que si le falta a esta tabla, y me parece que a todas las de internet, son referencias. Por ejemplo decir que u es una función (u=f(x), v=f(x), a=constante(un número) que pertenece a los reales (idem n))
está tabla de derivas tiene algunas que no son correctas, como por ejemplo:
la derivada de: y = x^n
no es y’ = n.x^n-1
sino que es y’= x’ n x^n-1
esta tabla no es apta.